Cube - Définition
 |
|
| Type | Polyèdre régulier |
|---|---|
| Faces | Carré |
| Éléments : · Faces · Arêtes · Sommets · Caractéristique |
6 12 8 2 |
| Faces par sommet | 3 |
| Sommets par face | 4 |
| Isométries | Oh |
| Dual | Octaèdre |
| Propriétés | Deltaèdre régulier et convexe, zonoèdre |
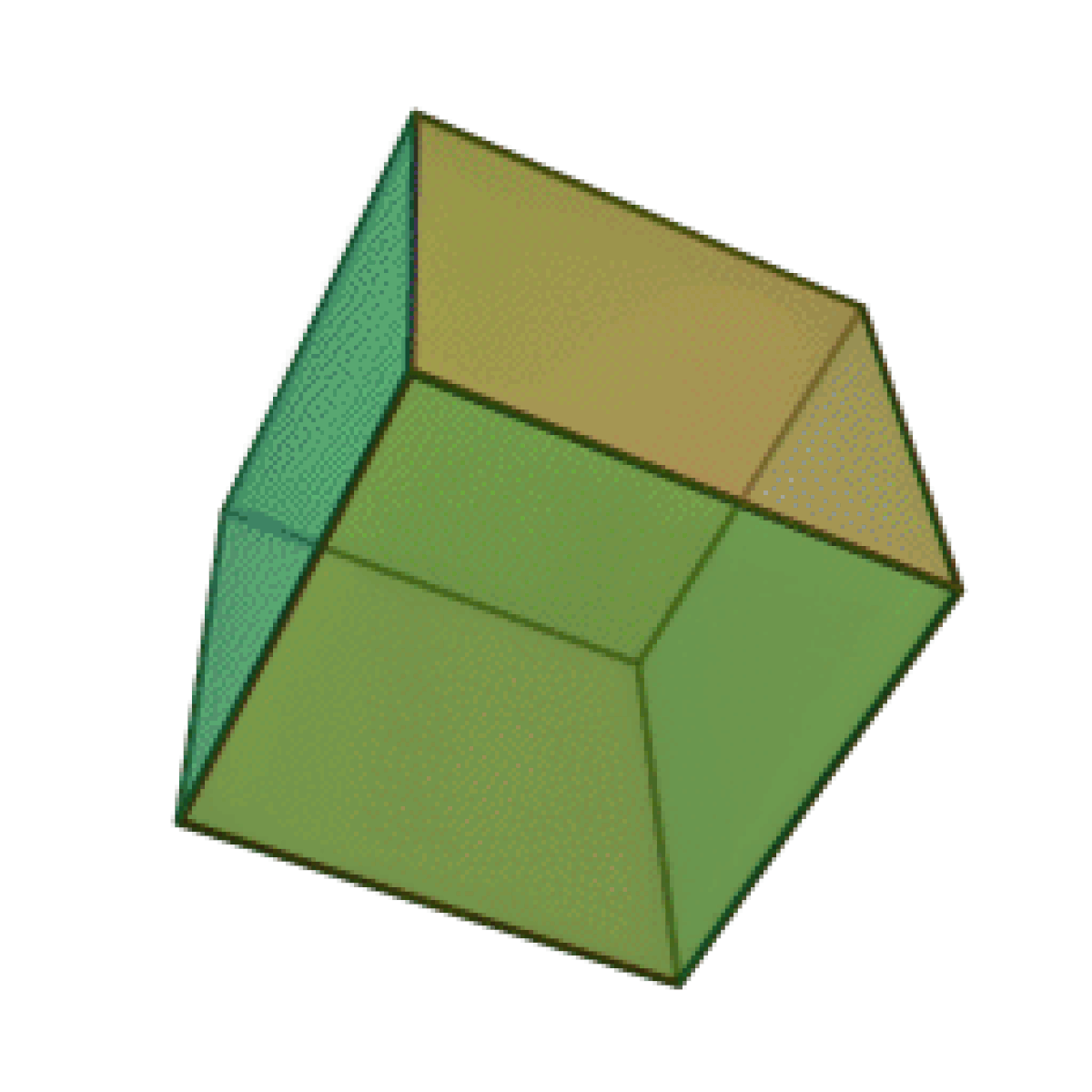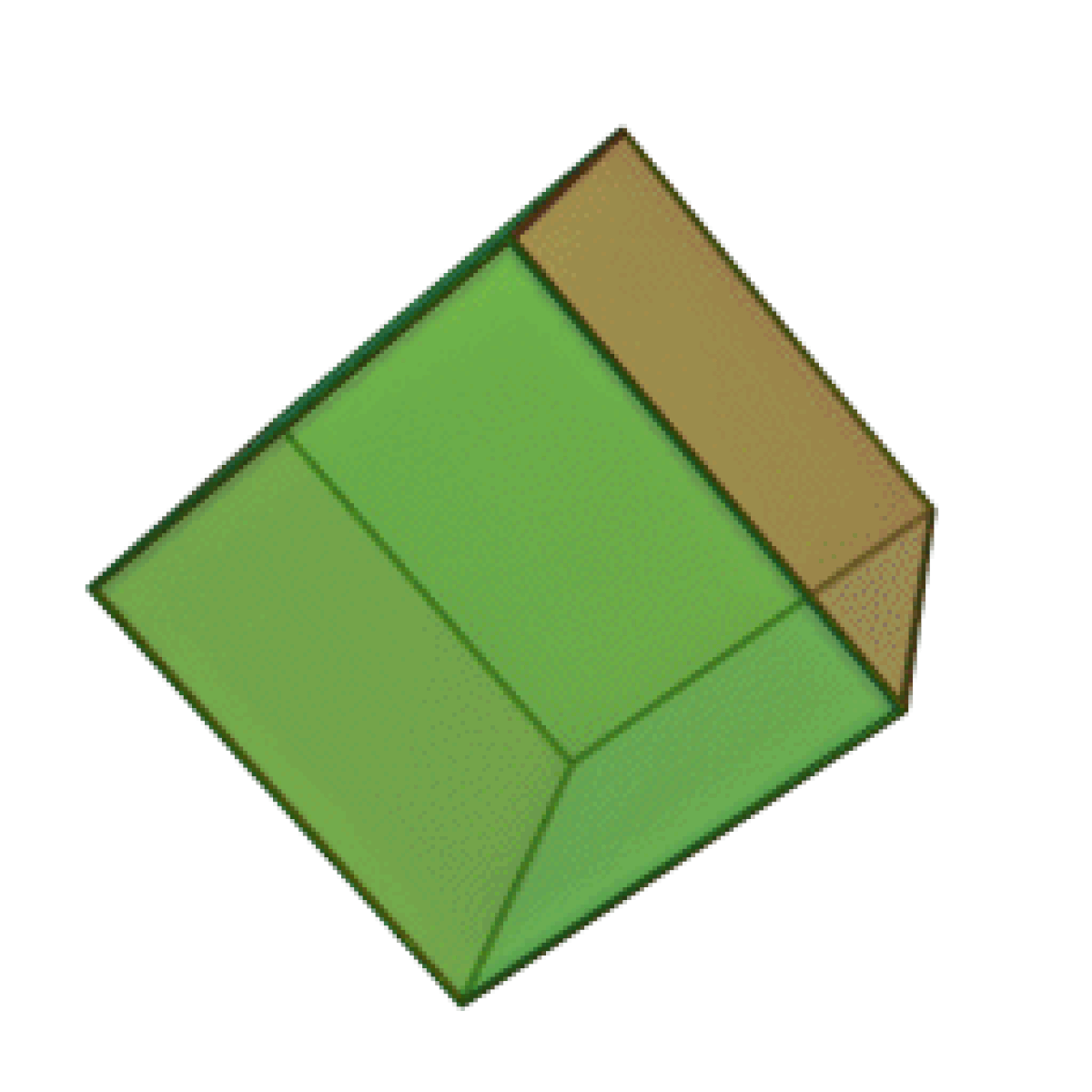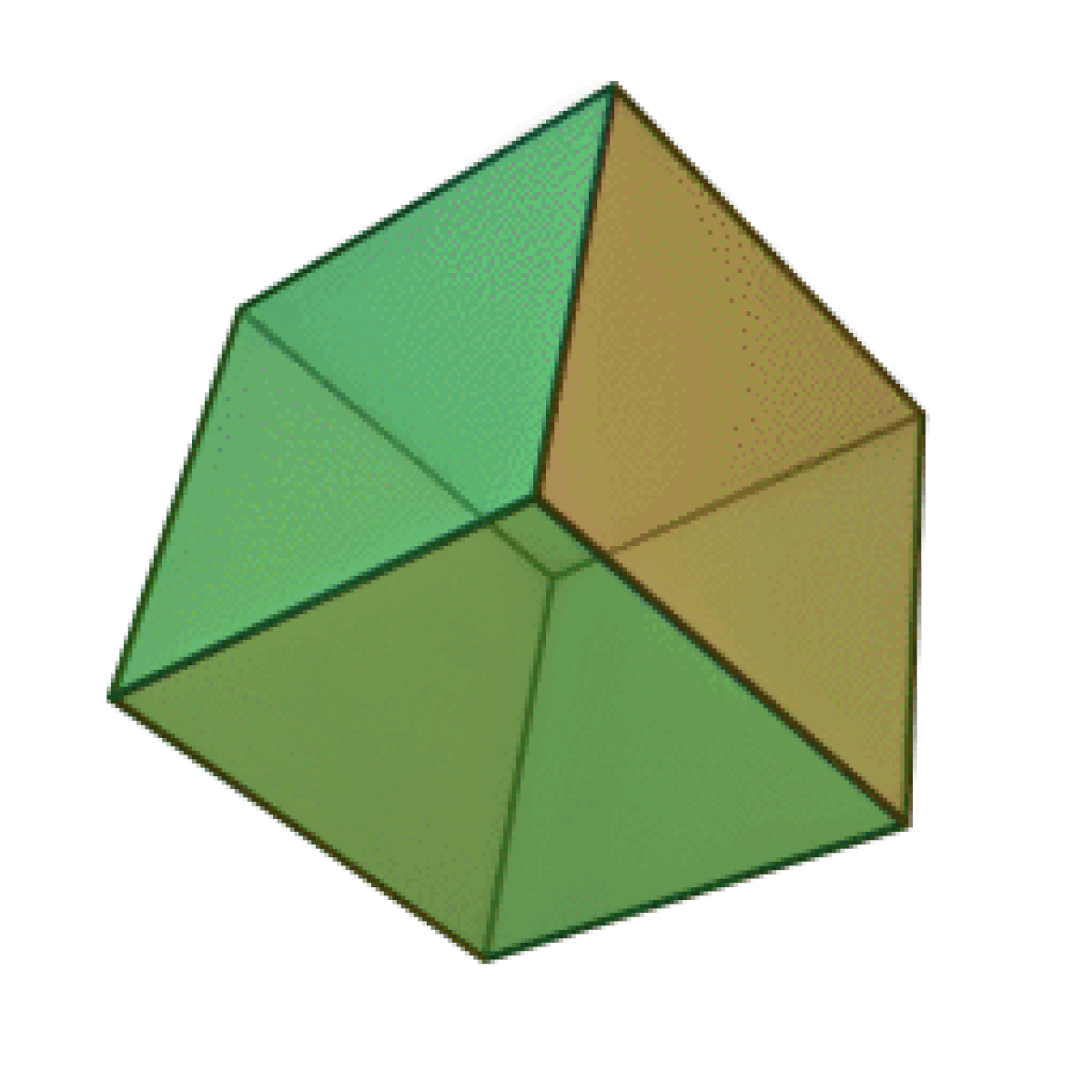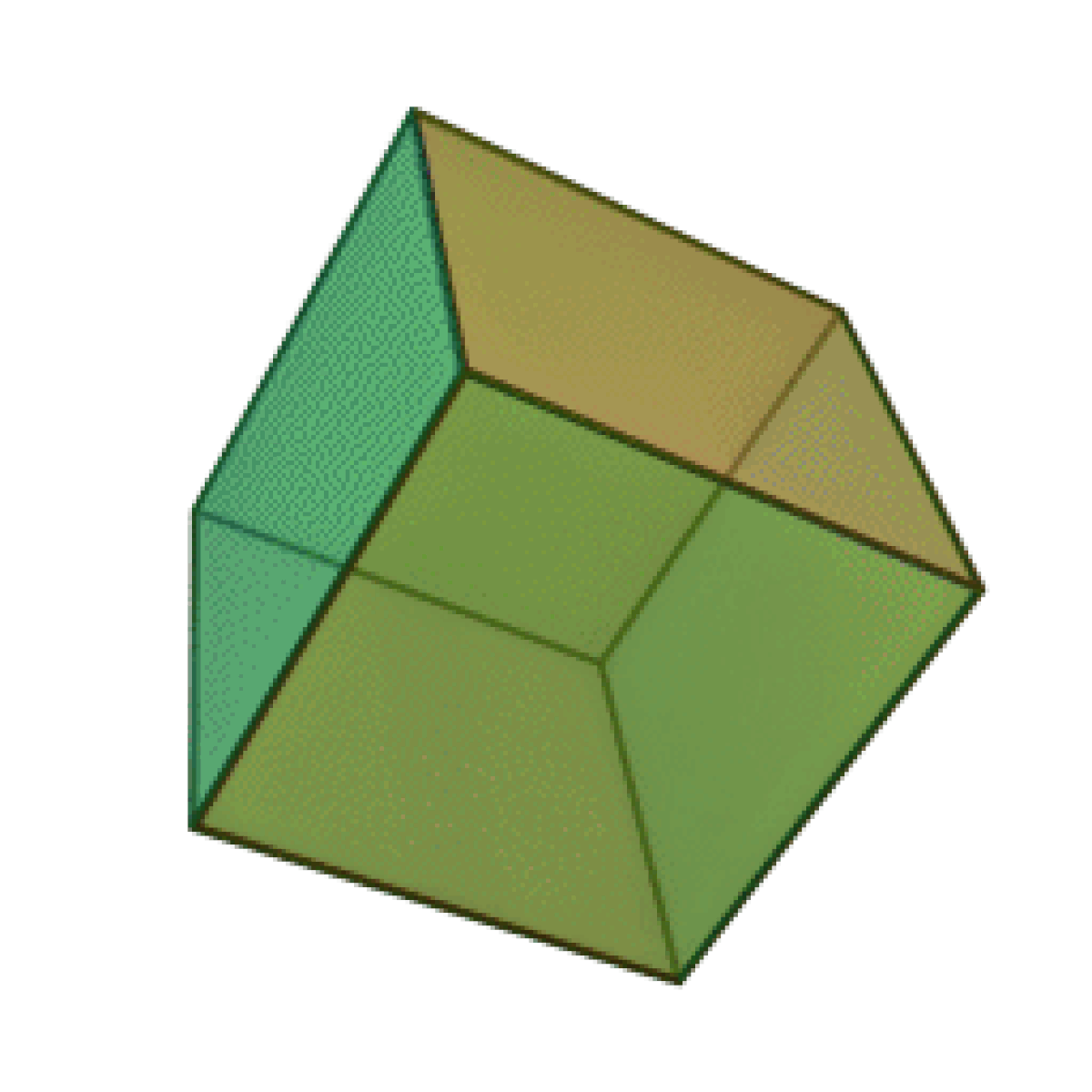
En géométrie élémentaire, un cube est un prisme dont les côtés sont tous égaux. Les cubes figurent parmi les solides les plus remarquables de l'espace. C'est un des solides de Platon. Son autre nom est " hexaèdre régulier ".
L'étymologie du terme cube est grecque ; cube provient de Kubos, le dé.
Géométrie
Le cube est un des cinq solides de Platon. Un cube appartient à la famille des prismes droits. Il possède 8 sommets et 12 arêtes. De plus :
- Deux arêtes ayant une extrémité commune sont orthogonales.
- Les faces opposées sont parallèles. Les faces adjacentes sont perpendiculaires
- Tous les angles dièdres sont droits.
- Les diagonales s'intersectent en un unique point, le centre de symétrie du cube, l'isobarycentre des huit sommets.
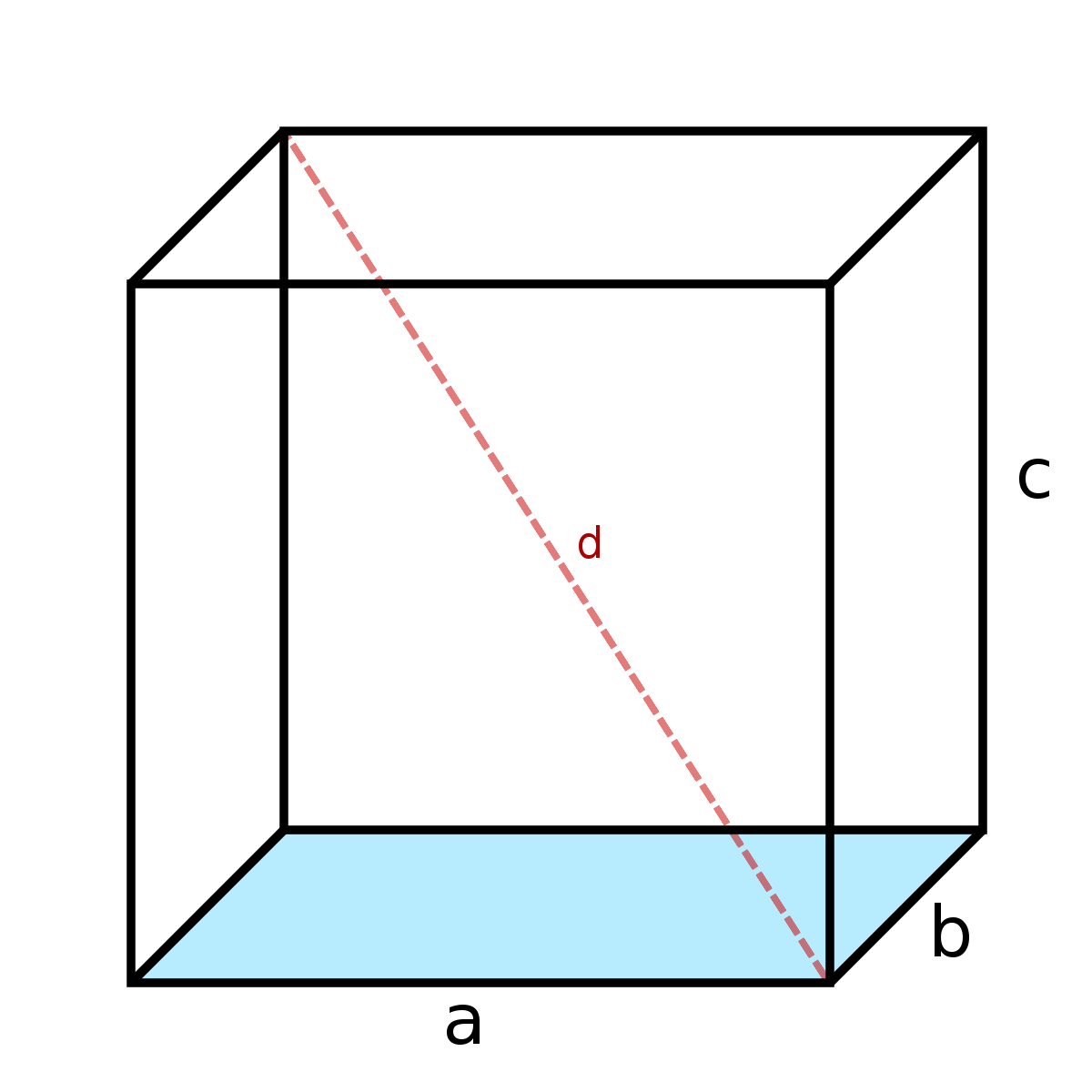
Mais par définition ses arêtes sont toutes de longueur égale, disons a. Ses faces sont donc des carrés, de même superficie, égale à a2. De fait :
- Son aire vaut donc 6 × a2.
- Son volume vaut a3.
- La longueur d'une diagonale vaut
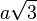
- La sphère circonscrite a donc pour rayon
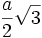
- La sphère tangente aux arêtes a pour rayon
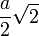
- La sphère inscrite a pour rayon
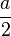
- L'angle entre la diagonale et chacun des plans adjacent vaut
C'est l'expression de son volume qui a conduit à l'utilisation du mot cube en algèbre.
Autres définitions
Il existe d'autres définitions équivalentes du cube :
- Les cubes sont les seuls polyèdres dont toutes les faces sont carrées.
- Le cube est un antidiamant d'ordre 3 à sommets réguliers et angles dièdre égaux.
Groupe des isométries
Le cube est l'un des polyèdres offrant le plus de symétries. Listons-les :
- 3 axes de rotation d'ordre 4 : axes passant par le centre de deux faces opposées.
- 6 axes de rotations d'ordre 2 : axes passant par le milieu de deux arêtes opposées
- 4 axes de rotation d'ordre 3 : axes passant par deux sommets opposés
- la symétrie de centre O
- 9 plans de symétrie : 3 plans médiateurs des arêtes, 6 plans passant par deux arêtes opposées.
Une isométrie du cube est entièrement définie par l'image d'un sommet et des trois arêtes issues de ce sommet (repère de l'espace). Ce sommet peut avoir pour image l'un quelconque des 8 sommets du cube. La première arête a alors 3 images possibles, la seconde arête deux images seulement et l'image de la dernière arête est alors déterminée. Ceci prouve que les isométries laissant le cube globalement invariant sont au nombre de 8 × 3 × 2 = 48. Ces isométries se partagent en 24 isométries positives et 24 isométries négatives. Les isométries positives possèdent toutes le point O comme invariant : on dénombre alors 23 rotations plus l'identité.
On retrouve alors les axes de rotations précédents :
- 3 axes de rotation générant 3 rotations d'angle non nul, soit 9 rotations
- 6 axes de rotation générant 1 rotation d'angle plat, soit 6 rotations
- 4 axes de rotation générant 2 rotations d'angle non nul, soit 8 rotations.
ainsi que les 9 symétries par rapport à un plan générées par les 9 rotations d'angle plat composées avec la symétrie de centre O.
Ce qui prouve que l'inventaire était bien exhaustif.
Patrons
Il existe de nombreux patrons du cube, onze différents pour être précis, en voici des exemples :

Développement en croix, les carrés latéraux peuvent être placés plus bas ou plus haut |

Développement en zigzag |
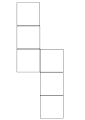
Ce développement tient dans un rectangle de deux sur cinq et minimise l'espace perdu |
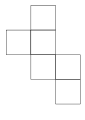
Le carré de gauche peut être placé plus bas ou plus haut |
Le cube et les autres polyèdres
Le dual du cube est l'octaèdre régulier. Ce qui explique que les deux solides possèdent le même groupe d'isométries.
Le cube s'inscrit dans un dodécaèdre régulier : les sommets du cube sont des sommets du dodécaèdre et les arêtes du cube sont formées de segments joignant deux sommets non consécutifs dans une face pentagonale du dodécaèdre. Il y a ainsi cinq façon d'inscrire un cube dans un dodécaèdre régulier.
On peut aussi inscrire le cube dans un dodécaèdre rhombique . Les sommets du cube correspondent aux sommets d'ordre 3 du dodécaèdre rhombique et les arêtes du cube correspondent aux diagonales des losanges.
Fascination du cube
Le cube a joué un rôle important dans la géométrie et la cosmologie grecque. Platon, dans le Timée le classe comme le quatrième solide, le premier construit à l'aide de triangles isocèles rectangles
" Groupés par quatre avec leurs angles droits se rencontrant au centre, ces triangles isocèles forment un quadrangle. Six de ces quadrangles en s'accollant ont donné naissance à huit angles solides, composés chacun de trois angles plans droits et la figure obtenue est un cube (Le Timée 54c - 55 d) "
Comme chaque solide de Platon, le cube est associé à un élément . Comme élément le plus stable, il est associé à la terre.
Le cube a été l'objet d'un problème qui s'est révélé insoluble : la duplication du cube à la règle et au compas.
Dans la cosmologie de Kepler, le cube est associé à la planète Saturne.
On retrouve aussi le cube dans la symbolique franc-maçonne. Le cube y symbolise les progrès que doivent faire le compagnon pour passer de la pierre brut au solide parfait.
Le cube a fait l'objet d'une séquence de trois films canadiens. Nintendo a produit la console GameCube. Le rubik's cube est un casse tête dont la réflexion se base sur des association sde couleur. Comprendre sa solution fait appel aux groupe des permutations.
On retrouve un cube tronqué dans le tableau mélancolia de Dürer. L'atomium de Bruxelles est un cube. En effet, le cube est un des réseaux possibles en cristallographie pour l'argent, l'or, le cuivre, le platine, le diamant, le sel.