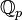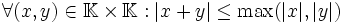Valeur absolue - Définition

Valeur absolue d'un nombre réel

Première approche

Un nombre réel est constitué de deux parties: un signe + ou - et une valeur absolue.

+ 7 est constitué du signe + et de la valeur absolue 7.

- 5 est constitué du signe - et de la valeur absolue 5.

La valeur absolue de (+ 7) est donc 7, la valeur absolue de (- 5) est donc 5.

Comme il est fréquent de supprimer le signe lorsque celui-ci est +, on obtient alors

• la valeur absolue de 7 est 7.
• la valeur absolue de (- 5) est 5, c'est-à-dire l'opposé de (- 5).

D'où la définition suivante.

Définition

Pour tout nombre réel x, la valeur absolue de x (notée |x|) est définie par :

• | x | = x, si x > 0
• | x | = − x, si x < 0
• | x | = 0, si x = 0

Nous remarquons que | x | = max( − x,x)

Propriétés

La valeur absolue d'un réel a les propriétés suivantes :

• 
• 
• 
• (si b ≠ 0)
• (inégalité triangulaire)
• (inégalité triangulaire généralisée à une famille finie (a_i))
• (deuxième inégalité triangulaire, découle de la première)
• 
• 
• ou

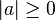
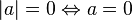
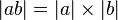
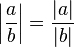
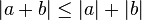
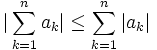
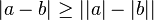
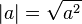
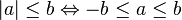
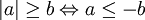
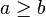
Ces dernières propriétés sont souvent utilisées dans la résolution des inéquations ; par exemple :

|x - 3| ≤ 9

-9 ≤ x - 3 ≤ 9

-6 ≤ x ≤ 12

Valeur absolue et distance

Il est utile d'interpréter l'expression |x - y| comme la distance entre les deux nombres x et y sur la droite réelle.

En munissant l'ensemble des nombres réels de la distance valeur absolue, il devient un espace métrique.

La résolution d'une inéquation telle que se résout alors simplement à l'aide de la notion de distance. La solution est l'ensemble des réels dont la distance au réel 3 est inférieure ou égale à 9. C'est l'intervalle de centre 3 et de rayon 9. C'est l'intervalle [3 - 9; 3 + 9] = [-6 ; 12].

Extension aux nombres complexes

La même notation s'emploie pour le module d'un complexe. Ce choix est légitime parce que les deux notions coïncident pour les complexes dont la partie imaginaire est nulle. En outre, le module de la différence de deux nombres complexes z₁ = x₁ + iy₁ et z₂ = x₂ + iy₂ est la distance euclidienne des deux points et .

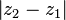
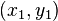
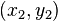
• Module de a + ib =
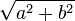
• Si b est nul, module de a = = valeur absolue de a

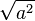
La fonction valeur absolue

Cette fonction fait correspondre à tout x, x si celui-ci est positif ou -x si celui-ci est négatif. La fonction valeur absolue est à valeurs positives, paire.

La fonction valeur absolue f définie par f(x) = |x| est continue sur et dérivable sur mais n'est pas dérivable en 0.

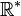
Sa représentation graphique est en forme de V:

Si f est une fonction,

• la fonction g définie par g(x) = f(|x|) est une fonction paire coïncidant avec f pour tout x de .
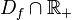
• la fonction h définie par h(x) = |f(x)| est une fonction coïncidant avec f pour tout x tel que et coïncidant avec - f pour tout x tel que

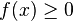
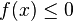
Valeur absolue dans un corps

Une valeur absolue définie sur un corps est une application qui à tout élément x de fait correspondre un nombre réel positif ou nul noté |x| de telle sorte que :

• (séparation) ;
• (inégalité triangulaire) ;
• 

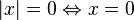
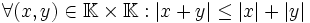
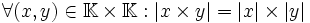
Une valeur absolue est dite ultramétrique si

On peut utiliser des valeurs absolues sur un anneau ou un groupe grâce à la valeur absolue induite sur ce groupe ou ce corps.

Exemples

• Le module défini sur est bien une valeur absolue d'où le fait qu'on utilise la même notation.
• La valeur absolue p-adique défini sur le corps (p un nombre premier) est une valeur absolue ultramétrique.