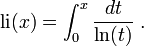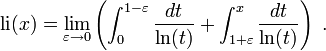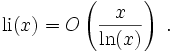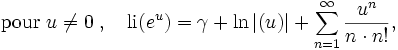Logarithme intégral - Définition
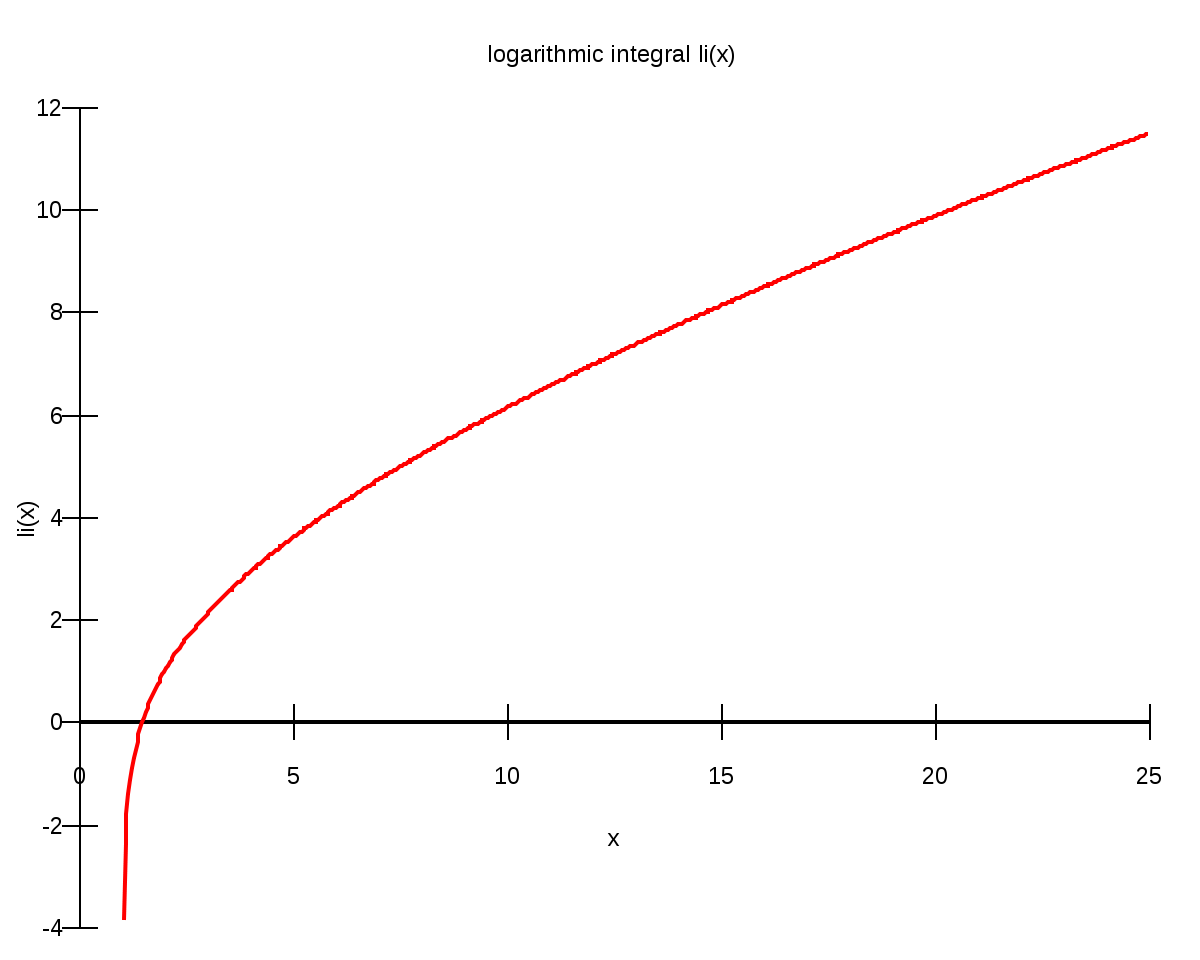
En mathématiques, le logarithme intégral li est une fonction spéciale définie en tout nombre réel strictement positif x≠ 1 par l'intégrale :
Ici, ln désigne le logarithme naturel. La fonction
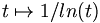
Le comportement de croissance de cette fonction pour x → ∞ est
(Voir Notation O).
Le logarithme intégral est important parce qu'il intervient dans les estimations de densité des nombres premiers, plus particulièrement dans le théorème des nombres premiers :
on a
- π(x) ~ Li(x)
où π est une fonction multiplicative; π(x) est égal au nombre de nombres premiers inférieurs ou égaux à x,
et Li est la fonction d'écart logarithmique intégrale, relativement à li définie par
Li(x) = li (x) - li(2).
L'écart logarithmique intégral donne une légèrement meilleure estimation de π que la fonction li. La fonction li est liée à l'exponentielle intégrale Ei par la relation
- pour tout nombre réel strictement positif x ≠ 1, li(x) = Ei (ln (x)).
Ceci mène aux développements en séries de li (x), par exemple:
où γ ≈ 0.57721 56649 01532... est la constante d'Euler-Mascheroni.
La fonction li a un seul zéro strictement positif; il se trouve en x ≈ 1.45136 92348...; ce nombre est connu comme étant la constante de Ramanujan-Soldner.