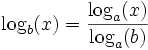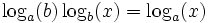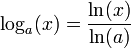Logarithme - Définition
En mathématiques, une fonction logarithme est une fonction définie sur
![] 0; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)

Les fonctions logarithmes les plus connues sont le logarithme décimal (ou logarithme de base 10) et le logarithme naturel ou népérien de base e. Les logarithmes ont été par la suite généralisés au plan complexe (logarithmes complexes) par prolongement analytique et introduits en théorie des groupes (logarithmes discrets) par analogie avec l'analyse.
On démontre que les fonctions logarithmes sont les réciproques des fonctions exponentielles.
Historique des logarithmes
En 1588, pour faciliter ses calculs, l'astronome suisse Jost Bürgi développa le premier système logarithmique connu.
Lorsqu'en 1614, John Napier ou Neper publie son traité Mirifici Logarithmorum Canonis Descriptio, il ne songe pas qu'il est en train de créer de nouvelles fonctions, mais seulement des tables de correspondances (logos = rapport, relation, arithmeticos = nombre) entre deux séries de valeurs possédant la propriété suivante : à un produit dans une colonne, correspond une somme dans une autre. Ces tables de correspondances ont été créées initialement pour simplifier les calculs trigonométriques apparaissant dans les calculs astronomiques et seront utilisées quelques années plus tard par Kepler. En 1619, apparaît une œuvre posthume de Neper Mirifici Logarithmorum Canonis Constructio, où il explique comment construire une table logarithmique (voir l'article table de logarithmes pour en comprendre le principe). Son travail sera poursuivi et prolongé par le mathématicien anglais Henry Briggs qui publie les tables de logarithmes décimaux et précise les méthodes d'utilisation des tables pour calculer des sinus, retrouver des angles de tangentes... Le logarithme décimal est parfois appelé logarithme de Briggs en son honneur.
En 1647, lorsque Grégoire de Saint-Vincent travaille sur la quadrature de l'hyperbole, il met en évidence une nouvelle fonction qui se trouve être la primitive de la fonction
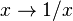
La notion de fonction, la correspondance entre les fonctions exponentielles et les fonctions logarithmes n'apparaissent que plus tardivement après le travail de Leibniz sur la notion de fonction (1697).
Logarithme décimal
- Voir article détaillé : logarithme décimal
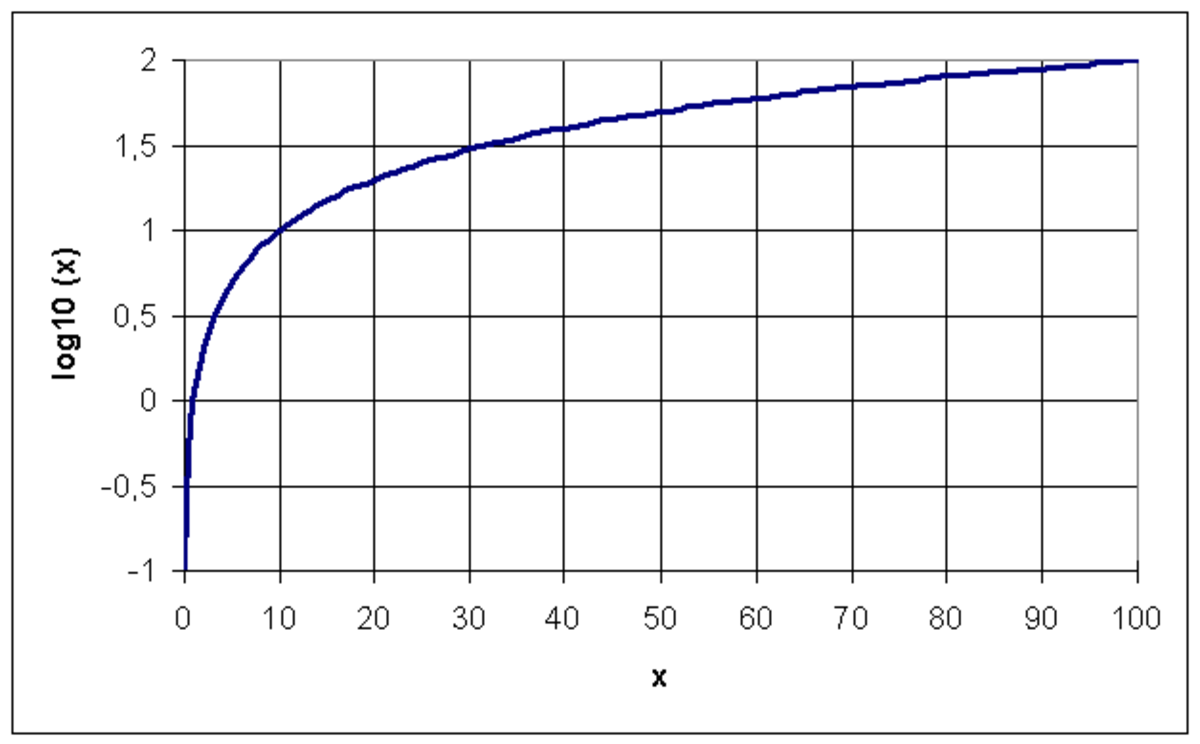
C'est le logarithme le plus pratique dans les calculs numériques, il est noté log ou log10. On le retrouve dans la création des échelles logarithmiques, les repères semi-logarithmiques ou log-log, dans la règle à calcul, dans le calcul du pH, dans l'unité du décibel.
Il précise à quelle puissance de 10 correspond un nombre :
- log(10) = 1, log(100) = 2, log(1000) = 3, log(0,01) = – 2.
Reste que la valeur du logarithme d'autres nombres que des puissances de 10 demande un calcul approché. Le calcul de log(2) par exemple peut se faire à la main, en remarquant que
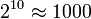
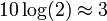
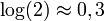
Logarithme naturel
- Voir article détaillé : logarithme naturel
C'est le logarithme dont la dérivée est la plus simple. C'est d'ailleurs le fait qu'il soit une primitive de
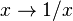
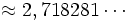
Remarque : ce logarithme est également nommé Logarithme népérien
Propriétés des fonctions logarithmes
Pour tout réel a strictement positif et différent de 1, le logarithme de base a :
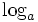
![]0 ; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)
-
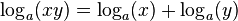
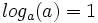
Cette définition permet de déduire rapidement les propriétés suivantes
-
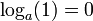
-
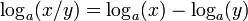
-
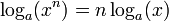
-
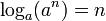
-
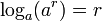
Comme tout réel x peut être considéré comme limite de termes de la forme , on détermine
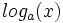
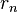
Deux fonctions logarithmes ne diffèrent que d'une constante multiplicative près:
En effet logb est la fonction continue qui transforme un produit en somme et qui vaut 1 en b, mais la fonction
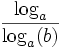
Toutes les fonctions logarithmes peuvent donc s'exprimer à l'aide d'une seule, une dont on connaît déjà la dérivée : ln
La fonction loga est dérivable de dérivée:
Elle est donc strictement monotone, croissante quand a est supérieur à 1, décroissante dans le cas contraire.
C'est une bijection dont la réciproque est la fonction
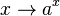
Curiosité mathématique: avec une erreur inférieure à 0,6%
-
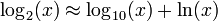
- Pour un inventaire de toutes les propriétés voir article détaillé : identités logarithmiques