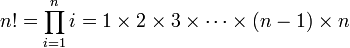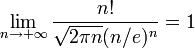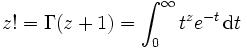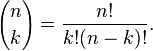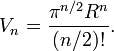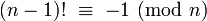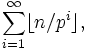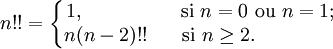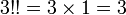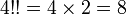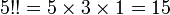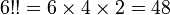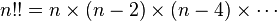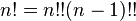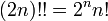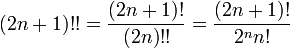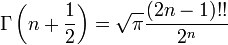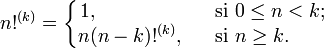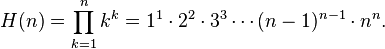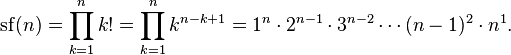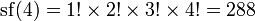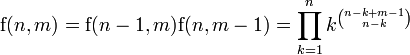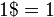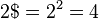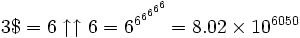Factorielle - Définition

En mathématiques, la factorielle d'un entier naturel n, notée n!, ce qui se lit soit " factorielle de n " soit " factorielle n ", est le produit des nombres entiers strictement positifs inférieurs ou égaux à n.

La factorielle joue un rôle important en algèbre combinatoire parce qu'il y a n! façons différentes de permuter n objets. Elle apparaît dans de nombreuses formules en mathématiques, comme par exemple la formule du binôme et la formule de Taylor.

Définition

Soit n un entier naturel. Sa factorielle est formellement définie par :

Par exemple :

• 1! = 1
• 2! = 1 × 2 = 2
• 3! = 1 × 2 × 3 = 6
• 10! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 = 3 628 800

Par convention :

0! = 1

La définition de la factorielle sous forme de produit rend naturelle cette convention puisque 0! est un produit vide, c'est-à-dire réduit à l'élément neutre de la multiplication. Cette convention est pratique pour deux points :

• Elle permet une définition récursive de la factorielle : (n+1)! = n! × (n+1) pour tout n.
• Elle permet à de nombreux identifés en combinatoire d'être valides pour des tailles nulles. En particulier, le nombre d'arrangements ou de permutations de l'ensemble vide est égal à 1.

La formule de Stirling donne un équivalent de n! quand n est grand :

d'où

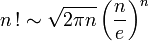
Généralisation

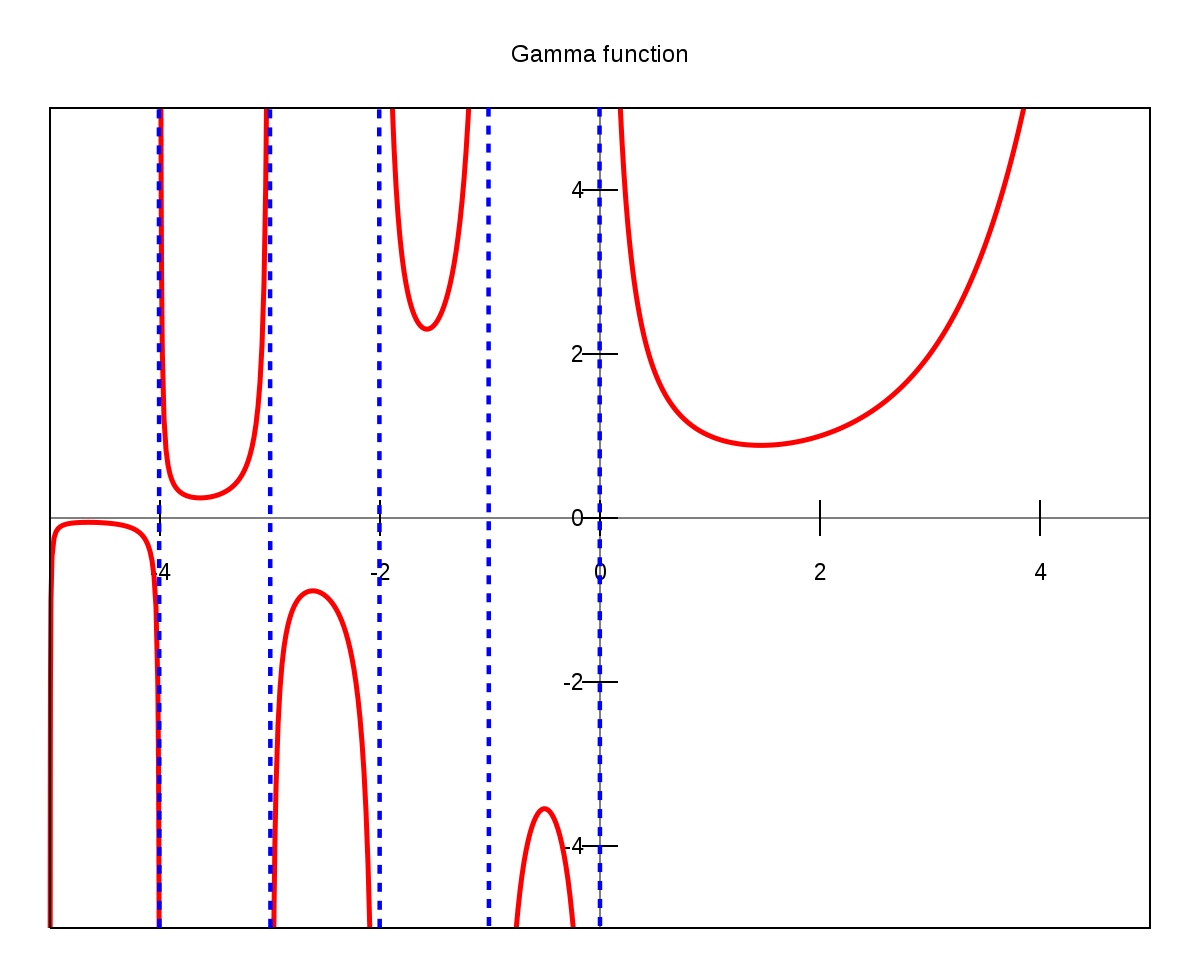
La fonction factorielle peut être prolongée à l'ensemble des nombres complexes (à l'exception des nombres entiers négatifs ou nuls) grâce à la fonction gamma d'Euler (notée Γ). En effet, pour n entier positif, on a :

Γ(n + 1) = n!

Par ailleurs, les deux fonctions satisfont les relations de récurrence suivantes :

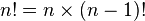
Γ(n + 1) = nΓ(n)

La fonction gamma agit donc comme un prolongement de la factorielle :

Cette fonction n'est cependant pas définie pour les nombres entiers négatifs ou nuls (0, -1, -2, etc.).

Cette vision de la fonction gamma comme prolongation de la factorielle est justifiée par les raisons suivantes :

• Les deux fonctions partagent une même définition récurrente.
• La fonction gamma est généralement utilisée dans un contexte similaire (même si plus général) à la factorielle.
• La fonction gamma est la seule fonction qui satisfait cette définition de récurrence sur les nombres complexes, qui est holomorphe et dont le logarithme de la restriction aux réels positifs est convexe (théorème de Bohr–Mollerup)

Applications

• En combinatoire, il existe n! façons différentes d'arranger n objets distincts (c’est-à-dire n! permutations). Et le nombre de façons de choisir k éléments parmi un ensemble de n est donné par le coefficient binomial :

• En permutation, si r éléments peuvent être choisis et arrangés de r façons différentes parmi un total de n objets (r < n), alors le nombre total de permutations distinctes est donné par :

_nP_r =

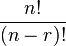
• Les factorielles apparaissent également en analyse. Par exemple, le théorème de Taylor, qui exprime la valeur en x d'une fonction f sous forme de série entière, fait intervenir la factorielle n! pour le terme correspondant à la n^e dérivée de f en x.

• Le volume d'une hypersphère en n dimensions peut être exprimé par :

• Les factorielles sont utilisées de façon intensive en théorie des probabilités.

• Les factorielles sont souvent utilisées comme exemple — avec la suite de Fibonacci — pour l'apprentissage de la récursivité en informatique du fait de leur définition récurrente simple.

Théorie des nombres

Les factorielles ont de nombreuses applications en théorie des nombres. Les nombres factoriels sont des nombres hautement composés. En particulier, n! est divisible par tous les nombres premiers qui lui sont égaux ou inférieurs. Par conséquent, tout nombre n > 4 est un nombre composé si et seulement si :

.

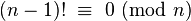
Un résultat plus fort est le théorème de Wilson. n est premier si et seulement si :

Adrien-Marie Legendre a montré que la multiplicité du nombre premier p dans la décomposition en produit de facteurs premiers de n! peut être exprimé par :

(qui est définie, car la fonction partie entière élimine tous les pⁱ > n).

La seule factorielle qui soit également un nombre premier est 2, mais il existe des nombres premiers de la forme , appelés nombres premiers factoriels.

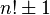
Programmation

La factorielle d'un nombre peut être calculée en utilisant un algorithme récursif ou itératif.

Écrivons en langage Scheme, proche du Lisp, un programme récursif donnant la factorielle d'un entier :

(define fact
(lambda (x)
(if (= x 0) 1
(* x (fact (- x 1))))))

Ce programme n'est pas efficace à l'exécution, pour les grands entiers.

De la même manière, en Caml :

let rec fact = function
| 0 -> 1
| n -> n * fact (n-1)

Ou de façon récursive terminale :

let fact n =
let rec aux r = function
| 0 -> r
| n -> aux (n*r) (n-1)
in
aux 1 n

En Haskell :

fact 1 = 1
fact n = n * fact ( n - 1 )

En Prolog :

fact(0,1).
fact(1,1).
fact(N,R):- N > 1, N1 is N - 1, fact(N1,R1), R is N*R1.

En langage C, de façon récursive :

int factorielle_recursive(int n)
{
if (n == 0)
return 1;
else
return n * factorielle_recursive(n-1);
}

Et de façon itérative :

int factorielle_iterative(int n)
{
int res;
for (res = 1; n > 1; n--)
res *= n;
return res;
}

En langage Python, de façon récursive :

fact = lambda x: x>0 and x*fact(x-1) or 1
----------------------------------------------------
Utilisation:
for i in range(10):
print "fact %d = %d" %(i, fact(i))
Ce qui produit à l'écran:
fact 0 = 1
fact 1 = 1
fact 2 = 2
fact 3 = 6
fact 4 = 24
fact 5 = 120
fact 6 = 720
fact 7 = 5040
fact 8 = 40320
fact 9 = 362880

Ces fonctions ne permettent pas de calculer la factorielle d'un nombre supérieur à 12 si les entiers sont limités à 32 bits, car le résultat dépasse la place disponible. De plus, par souci de clarté, les programmes ci-dessus sont dépourvus de traitement des entrées-sorties.

Variantes

Primorielle

La fonction primorielle est similaire à la fonction factorielle, mais ne prend en compte que le produit des nombres premiers.

Multifactorielles

Afin d'alléger l'écriture, une notation courante est d'utiliser plusieurs points d'exclamation pour noter une fonction multifactorielle, le produit d'un facteur sur deux (n!!), sur trois (n!!!) ou plus.

n!!, la double factorielle de n, est définie de façon récurrente par :

Par exemple :

• 
• 
• 
• 
• 

Certaines identités découlent de la définition :

Il faut faire attention de ne pas interpréter n!! comme la factorielle de n!, qui serait écrite (n!)! et est un nombre largement plus grand. Certains mathématiciens ont suggéré la notation alternative n!₂ pour la double factorielle et similairement n!_n pour les autres multifactorielles, mais cet usage ne s'est pas répandu.

La double factorielle est la variante la plus commune, mais il est possible de définir de façon similaire la triple factorielle, etc. De façon générale, la k^e factorielle, notée n!^(k), est définie de façon récurrente par :

Hyperfactorielle

L'hyperfactorielle de n, notée H(n), est définie par :

Pour n = 1, 2, 3, 4,... les valeurs de H(n) sont 1, 4, 108, 27 648,... (la séquence A002109 de l'OEIS).

La fonction hyperfactorielle est similaire à la fonction factorielle, mais produit de plus grands nombres. Sa croissance est en revanche comparable.

Superfactorielle

Neil Sloane et Simon Plouffe ont défini la superfactorielle en 1995 comme le produit des n premières factorielles :

Par exemple, la superfactorielle de 4 est :

La suite des superfactorielles débute (depuis n = 0) par :

1, 1, 2, 12, 288, 34560, 24883200, ... voir (la séquence A000178 de l'OEIS)

L'idée fut étendue en 2000 par Henry Bottomley à la superduperfactorielle, produit des n premières superfactorielles, débutant (depuis n = 0) par :

1, 1, 2, 24, 6912, 238878720, 5944066965504000, ... voir (la séquence A055462 de l'OEIS)

puis, par récurrence, à n'importe quelle factorielle de niveau supérieur, où la factorielle de niveau m de n est le produit des n premières factorielles de niveau m-1, c’est-à-dire, en notant f(n,m) la factorielle de n de niveau m :

où f(n,0) = n pour n > 0 et f(0,m) = 1.

Superfactorielle (définition alternative)

Clifford Pickover, dans son livre Keys to Infinity (1995), définit la superfactorielle de n, notée n$ ($ étant un signe factoriel ! portant un S superposé), comme :

,

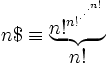
ou, en utilisant la notation de Knuth :

.

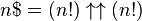
Les premiers éléments de la suite des superfactorielles sont :