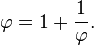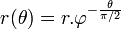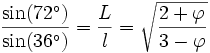Nombre d'or - Définition
Le nombre d'or, habituellement désigné par la lettre φ (phi) de l'alphabet grec en l'honneur de Phidias, sculpteur et architecte grec du Parthénon, est le nombre irrationnel :
-
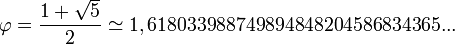
Propriétés algébriques
Équation
C'est l'unique racine strictement positive de :
-
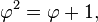
On peut aussi écrire le nombre d'or en fonction du nombre π :
-
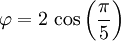
Et même en fonction du i des complexes et de e appelé nombre exponentiel par Euler :
-
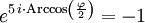
-
Puissances du nombre d'or
-
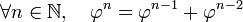
En effet, il suffit de multiplier l'égalité
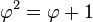

Ou encore :
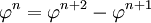
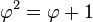
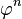
Cette relation de récurrence est à rapprocher de celle qui relie les nombres de Fibonacci
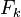
-
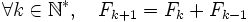
Proportions
Deux nombres sont dits être dans le rapport du nombre d'or ou dans la divine proportion, si le tout par rapport au plus grand est comme le plus grand par rapport au plus petit, id est :
-
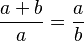
De manière équivalente, ils sont dans le rapport du nombre d'or si le rapport du plus grand par le plus petit est égal au rapport du plus petit par leur différence :
-
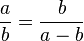
De simples manipulations algébriques, (multiplication de la première par a/b et de la seconde par (a-b)/b), montrent que ces deux relations sont équivalentes à :
-
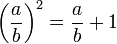
et ainsi :
-
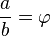
Le fait qu'un segment soit divisé en deux morceaux de longueurs a et b qui restent dans le rapport du nombre d'or est aussi (d'après Euclide) exprimé comme " la longueur est coupée en extrême et moyenne raison ".
Suite de Fibonacci
- Voir article détaillé : Suite de Fibonacci
L'expression explicite des termes d'une suite de Fibonacci utilise le nombre d'or et son inverse. Cette suite commence par f0 = 0,f1 = 1,f2 = 1, puis 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946...
La relation de récurrence est fn = fn − 1 + fn − 2. Les suites géométriques vérifiant cette relation de récurrence sont des suites
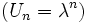
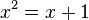

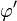
-
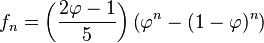
Grâce à cette expression, on peut prouver que la limite des rapports des termes successifs de la suite de Fibonacci est égale au nombre d'or.
Écritures possibles
Puisque φ est défini comme étant la racine d'une équation polynomiale, c'est un nombre algébrique. Il peut être montré que φ est un nombre irrationnel.
Comme
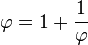
-
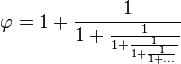
Comme
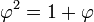
-
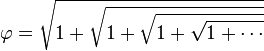
Le nombre d'or a des propriétés intéressantes lorsqu'il est utilisé comme base d'un système de nombre (voir base d'or).
Extension algébrique
Un aspect fascinant du nombre d'or est que l'on a l'impression de tourner sans fin dans un labyrinthe d'équations de plus en plus mystérieuses (voir les chapitres mathématiques de The divine proportion, 1970, HE Huntley). On peut dissiper le mystère :
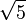

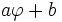
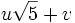
L'ensemble des nombres de la forme
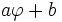
![\mathbb Q[\varphi]](https://static.techno-science.net/illustration/Definitions/autres/e/e0a31a47addc13fe8cf79b92ad6d11f9_fd956da5a608588dbef256b6163a06c1.png)

En particulier, tout polynôme à coefficients rationnels en

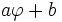


L'ensemble des nombres de la forme
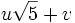
![\mathbb Q[\sqrt 5]](https://static.techno-science.net/illustration/Definitions/autres/8/86faffa9d5d2ef1b16b5f38d8c59f94e_c4955a291dcbd438550dd4fa0eda40fd.png)
La relation entre

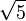
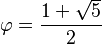
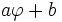
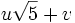
- Dans un sens :
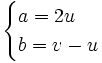
- Dans l’autre sens :
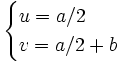
![\mathbb Q[\varphi]](https://static.techno-science.net/illustration/Definitions/autres/e/e0a31a47addc13fe8cf79b92ad6d11f9_fd956da5a608588dbef256b6163a06c1.png)
- Cet ensemble est stable pour l'addition car
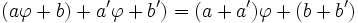
- Il est stable pour la soustraction pour les mêmes raisons.
- Il est stable pour la multiplication car \varphi^2 = \varphi + 1 donc
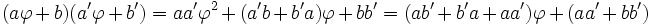
- il est stable par la prise de l'inverse. En effet l'égalité
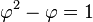
-
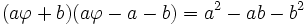
-
- Il suffit alors, dans un fraction dont le dénominateur est
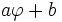
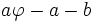
-
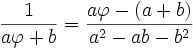
-
- avec les cas particuliers :
-
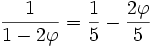
-
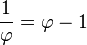
-
Tout polynôme en

- Il suffit d’utiliser en cascade l’équation :
-
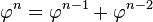
-
![\mathbb Q[\sqrt 5]](https://static.techno-science.net/illustration/Definitions/autres/8/86faffa9d5d2ef1b16b5f38d8c59f94e_c4955a291dcbd438550dd4fa0eda40fd.png)
- Les démonstrations sont analogues au précédent à ceci près que, dans une fraction dont le dénominateur est
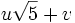
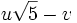
![\mathbb Q[\sqrt 5] = \mathbb Q[\varphi].](https://static.techno-science.net/illustration/Definitions/autres/5/568a4f5d90febe3722192c90bd3b158d_ec4eccb12629752323f8a67e24a468d6.png)
- De l'égalité
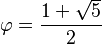
-
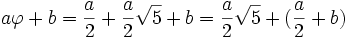
-
- De l'égalité
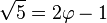
-
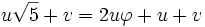
-
En revanche, ces corps ne sont pas stables par la prise de la racine carrée. Cependant, on peut noter quelques résultats remarquables :
- Les racines carrées stables :
-
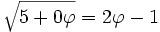
-
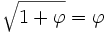
-
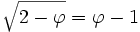
- Les nombres de Fibonacci procurent quelques belles racines,
-
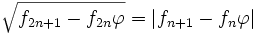
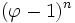
- par exemple :
-
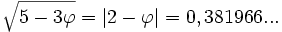
-
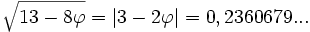
-
- racines carrées stables à un facteur
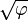
-
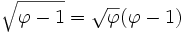
-
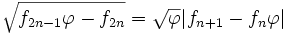
Remarque
On pourrait imaginer un nouveau nombre d’or ? à partir d’une des solutions irrationnelles d’une équation du second degré à coefficients rationnels, puis trouver de nombreuses propriétés concernant ses polynômes, construire des figures géométriques où il serait présent, trouver un angle dont le cosinus aurait aussi une relation avec lui. Ceci nous laisserait pantois, mais il serait peut-être moins doré que

Propriétés géométriques
Rectangle d'or
On appelle rectangle d'or un rectangle dont le rapport entre la longueur et la largeur vaut le nombre d'or.
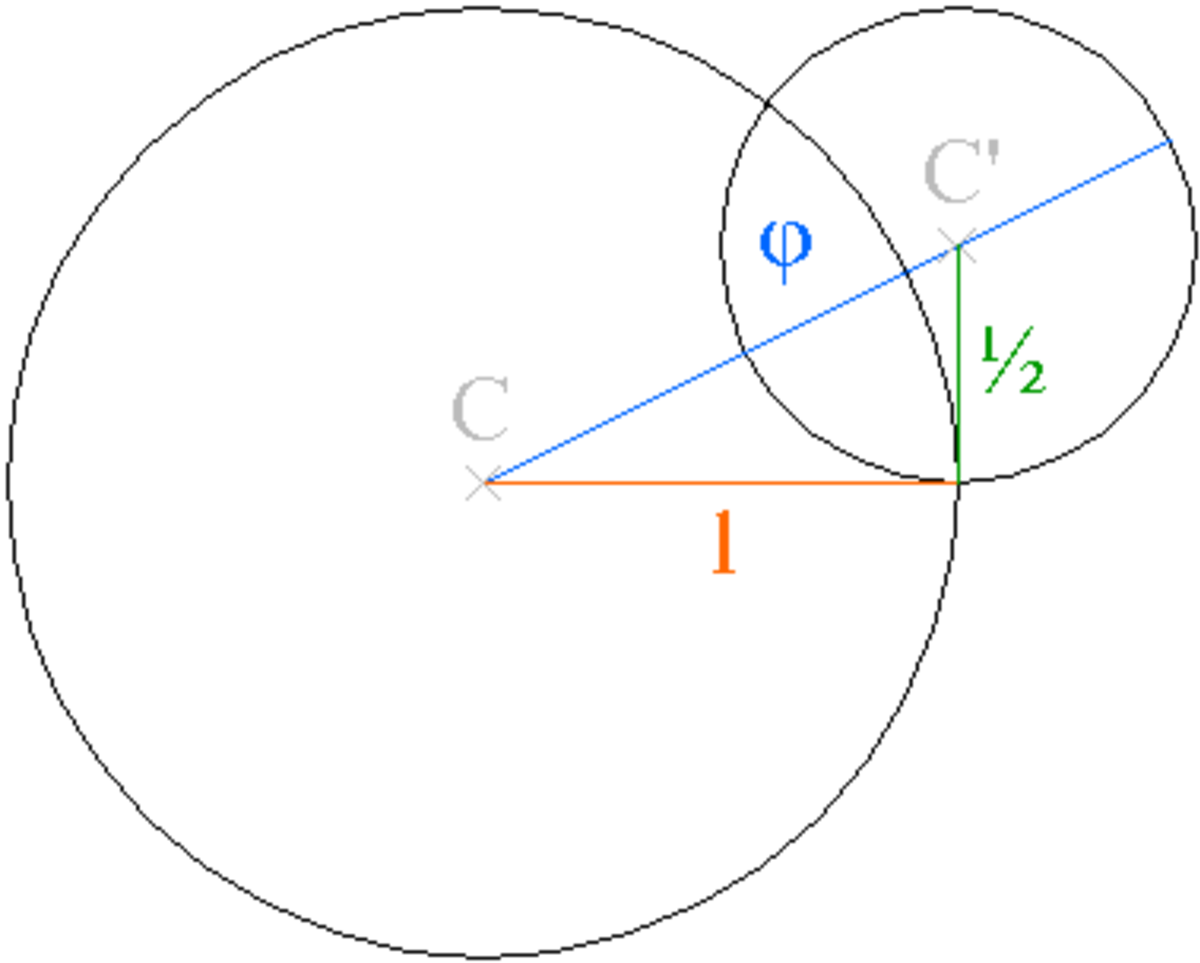
Le tracé d'un rectangle d'or se fait très simplement à l'aide d'un compas; il suffit de pointer le milieu d'un côté d'un carré, de pointer l'un des deux angles opposés, puis de rabattre l'arc de cercle sur la droite passant par le côté du carré pointé. (ceci est un " secret " de compagnonnage)
Voici une raison possible de l'attrait suscité par le rectangle d'or : considérons un rectangle dont les côtés de longueurs a et b sont dans un rapport du nombre d'or :
Si de ce rectangle, nous supprimons le carré de côté de longueur b, alors le rectangle restant est à nouveau un rectangle d'or, puisque ses côtés sont dans un rapport φ. En effet, d'après les propriétés algébriques,
-
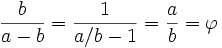
En itérant cette construction, nous obtenons une suite de rectangles d'or de plus en plus petits.
Triangles d'or
Les triangles d'or sont des triangles isocèles dont le rapport des côtés est égal au nombre d'or. Il en existe de deux types. Ceux pour lesquels le rapport côté / base vaut φ qui donnent des triangles aigus appelés parfois triangles d'argent et ceux pour lesquels le rapport base / côté vaut φ.
Dans la figure jointe :
- Les triangles isocèles BDA et CAB ont un angle de base commun en A. ABD est donc semblable à BCA dans un rapport de 1/φ.
- Comme φ = 1+ 1/φ, DC = 1 et DBC est isocèle de sommet D.
- L'angle en B est donc double de l'angle en C dans ABC.
- La somme des angles d'un triangle valant 180°, on obtient pour l'angle C le cinquième de l'angle plat, soit 36° et pour l'angle B les deux cinquièmes de l'angle plat, soit 72°.
Puisqu'il s'agit de découper un angle plat en 5, il n'est pas surprenant de retrouver ces triangles d'or dans le pentagone régulier et dans le pentacle.
Dans un triangle d'or aigu, on peut dessiner un triangle d'or obtus et un triangle d'or aigu φ fois plus petit. On retrouve ce même phénomène dans un triangle d'or obtus. Ces faits expliquent que l'on retrouve ces deux éléments dans les pavages de Penrose
Spirales d'or
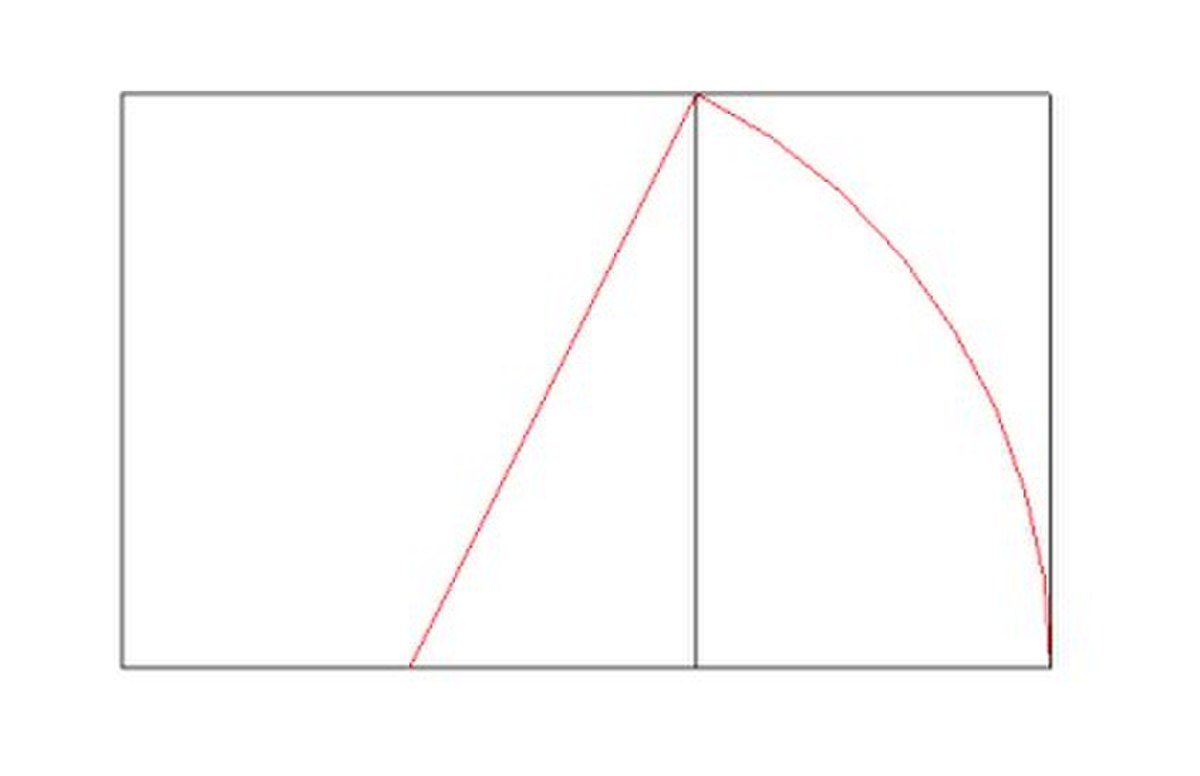
On peut construire, à partir d'un rectangle d'or, une spirale d'or en traçant des quarts de cercle dans chaque carré. Cette spirale se rapproche d'une spirale logarithmique de centre l'intersection des deux diagonales des deux rectangles et d'équation polaire :

|
On peut construire, à partir du triangle d'or, une spirale d'or triangulaire rappelant certaines images astrophysiques et se rapprochant d'une spirale logarithmique d'équation polaire
-
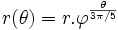
Nombre d'or et pentagone
On a déjà pris conscience que le nombre d'or, par le biais des triangles d'or, était en relation avec les angles de 36° (le cinquième d'un angle plat). On va voir ici qu'il est en relation avec les distances dans un pentagone et un décagone.
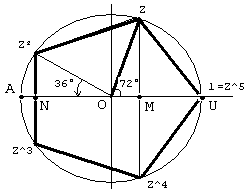
Dans le pentagone ci-dessus, les points Z et Z2 ont respectivement pour abscisse cos(72°) et cos(144°). Une incursion dans les nombres complexes permet de prouver :
-
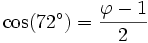
-
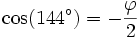
puis par considération géométrique :
-
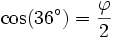
Les cosinus de 0°, 72°, 144°, 216°, 288° (notés x) et leurs sinus (notés y) sont les solutions de l'équation
- (x + iy)5 = 1.
A première vue il faudrait résoudre l'équation de degré 5 :
-
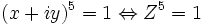
Remarquons que Z2 est le conjugué de Z3 donc que ces deux nombres ont même partie réelle :
- La partie réelle de Z2 est :
-
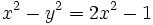
- La partie réelle de Z3 est :
-
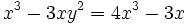
L'égalité des deux parties réelles revient à résoudre :
-
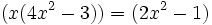
-
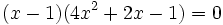
-
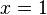
-
- ou bien :
-
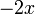
-
Les solutions correspondent aux abscisses des 3 points U, Z, Z2, d'où les valeurs trouvées.
Les carrés des sinus peuvent être calculés élégamment par les puissances des points M et N par rapport au cercle unitaire.
On obtient alors les valeurs suivantes :
-
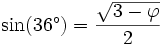
-
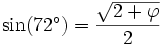
-
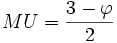
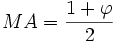
-
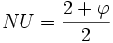
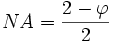
Donc :
-
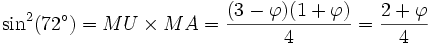
-
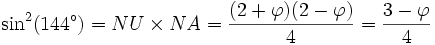
De ces égalités on peut alors déduire directement la longueur des côtés du pentagone,
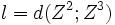
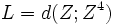
-
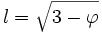
-
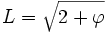
Ceci met en évidence des triangles d'or car le rapport entre ces deux grandeurs se calcule ainsi
le rapport en question se calculant par la formule de l'inversion du binôme,
-
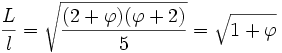
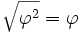
ce qui revient à dire que le triangle isocèle U-Z-Z4 est d'or, ainsi que U-Z2-Z3.
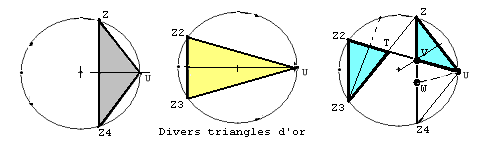
Des considérations de symétrie montrent que UZV et T-Z2-Z3 sont isocèles, de plus ils sont semblables aux deux précédents, dans un rapport de similitude égal à l'inverse de

Nombre d'or et fonction trigonométrique
Le paragraphe précédent a permis de mettre en place le cosinus et le sinus du cinquième de l'angle plat (36°). À partir de cette valeur et en appliquant la formule de l'angle moitié :
-
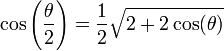
ainsi que les formules d'angle double et d'angle complémentaire, on peut déterminer le cosinus de tous les angles multiples de 9° :
-
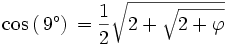
-
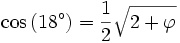
-
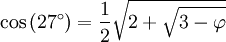
-
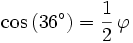
-
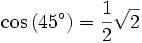
-
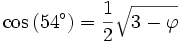
-
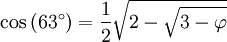
-
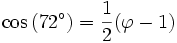
-
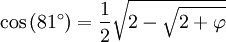
On peut aussi déterminer le cosinus des angles de la forme
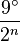
-
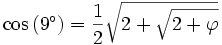
-
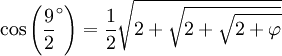
-
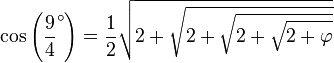
-

Si ce processus se poursuit indéfiniment l'angle devient nul d'où :
-
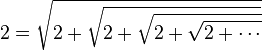
- ce qu'on savait déjà, voir itération infinie de racines carrées.
Le nombre d'or dans l'art : mythe ou réalité ?
Les débuts du nombre d’or
Euclide l'appelle la proportion de moyenne et extrême raison. Les Pythagoriciens en font un symbole de leur secte avec la figure géométrique qui lui est associée : le pentacle. Léonard de Pise le retrouve dans les suites qui portent son nom. Le moine mathématicien italien Luca Pacioli lui consacre un livre intitulé De divina proportione rédigé en 1498 avec la collaboration de Léonard de Vinci pour les figures. Johannes Kepler dit de lui
" La géométrie a deux grands trésors : l'un est le théorème de Pythagore; l'autre la division d'un segment en moyenne et extrême raison. Le premier, nous pouvons le comparer à une mesure de l'or ; le second nous pouvons l'appeler un précieux bijou. "
La découverte de sa présence presque parfaite dans le Parthénon construit par Phidias fait qu'on lui attribue, en son honneur, la lettre φ comme nom. Cette proportion souvent considérée comme esthétique est étudiée ensuite par Charles Henry et Georges Seurat. Une exposition, ‘’la section d'or’’, lui est consacrée en 1912.
La contribution de Ghyka
Vers 1930, le Roumain Matila Ghyka voit le nombre d'or partout : les spirales des coquillages, la disposition des feuilles des plantes, le nombre de pétales... mais aussi l'architecture ou la peinture. C'est lui qui popularise cette notion que les rectangles construits à partir du nombre d'or sont attrayants visuellement. Ghyka trouve en effet des approximations de φ par exemple dans des tableaux comme la Joconde.
Des travaux critiqués
- Ses mesures seraient approximatives. Il semble qu’il ne trouve qu’environ 1,6.
- Ses résultats sont trop souvent complexes. Selon ses détracteurs, il faut décortiquer dans tous les sens un portrait pour y trouver lesdites valeurs. Selon ses partisans, le nombre de ses découvertes dans une seule œuvre excuse la difficulté que l’on peut avoir à les retrouver.
- Certains poussent le raisonnement jusqu’à dire que ses résultats n’ont rien à voir avec une décomposition normale d’un tableau ou d’un monument.
- L'exemple du Parthénon, très populaire, serait ainsi biaisé : pour obtenir un vrai rectangle d'or, on ne prend pas la façade, mais la façade plus quelques marches pour avoir la bonne hauteur et donc le bon rapport ! De plus, pour les mesures effectuées avec le chapiteau, les détracteurs soulignent le fait que celui-ci étant écroulé, on n’en connaît pas la hauteur originale, ce à quoi les partisans répondent que prolonger sur un plan les droites formées par les morceaux restants suffit.
- L’exemple de la Grande Pyramide se baserait sur un récit d’Hérodote, mais quand on examine le texte en question on se rend compte qu'il ne comporte aucun détail mathématique de ce genre.
- L’exemple également assez répandu de Saint-Jérôme (détail du tableau éponyme de Léonard de Vinci) ne prouverait rien : le personnage est si mal encadré par le rectangle d’or (noté ici en bleu) que son bras droit n’y est pas inclus entièrement, prouvant ainsi malgré ses partisans que le nombre d’or n'a pas été utilisé par le peintre. Les partisans considèrent au contraire que la partie majeure du corps est bien enserrée dans le rectangle et que le bras compte bien moins que la masse formée par le corps accroupi.
- Nous pourrions ainsi multiplier les exemples, avec arguments et contre-arguments à l’appui.
- Ghyka travaillait sur des copies en noir et blanc des œuvres. Or un tableau, un monument, c'est bien plus qu'une construction géométrique. Ce sont des couleurs, des matières... L'attrait des spectateurs pour telle œuvre a probablement d’autres explications que l'existence prouvée ou non de rapports géométriques.
Au-delà de la méthode
Le lecteur est alors en droit de se demander ce qu’il adviendrait si les résultats étaient exacts et se rapportaient à des découpages cohérents et reconnus des œuvres étudiées. Plusieurs pistes tendent à montrer que cela ne prouverait rien quand même.
Une des études statistiques les plus connues est celle du philosophe allemand Gustav Fechner, réalisée en 1876. Il se base sur des formes élémentaires et recherche dans les croix du commerce (bijoux) ou religieuses (crucifix et croix tombales) les proportions les plus courantes. Il en présente à un grand nombre de personnes plusieurs modèles et leur demande de choisir celle qui à leurs yeux est la plus esthétique. La croix considérée comme la plus esthétique est celle de Saint-André.
La seconde expérience réalisée par Fechner porte sur différents rectangles. Sa procédure consiste à présenter à un sujet une série de dix rectangles dont les rapports hauteur/largeur varient entre 1 et 0,4. Le sujet doit ensuite choisir la figure qui lui paraît la plus esthétique. Environ 76% des choix sont centrés sur des rectangles dont les rapports sont 0,57 ; 0,62 et 0,67. Les autres figures reçoivent moins de 10% chacune.
Ces considérations ne peuvent donner une réponse absolue quant à la présence du nombre d’or en esthétique. Mais les résultats obtenus vont néanmoins dans le sens de la ‘’divine proportion’’. Malgré cela, les choix de Fechner sont relativement limités et l’ordre de présentation des rectangles joue un rôle important sur le choix des sondés.
Un test réalisé par George Markowsky met en œuvre 48 rectangles de proportions différentes (entre 0,4 et 2,5). La hauteur de ces figures est fixe, seule la largeur varie. Les rectangles sont tout d’abord présentés sous forme de matrice 6x8 et organisés de manière aléatoire. Il en ressort que la plupart des gens sont incapables de trouver le rectangle d’or dans ces conditions. Les figures sont ensuite ordonnées selon leur largeur dans l’ordre croissant. Il se trouve que dans cette configuration, les choix sont relativement différents par rapport au cas précédent. Dans cette expérience, le rectangle le plus souvent nominé est celui dont le rapport est de 1,83. Ce test semble prouver que le rectangle d’or n’est pas celui qui nous paraît le plus esthétique.
Autres contributions
Le mathématicien H.E. Huntley publie en 1970 The Divine Proportion. A Study in Mathematical Beauty où il expose toutes les situations où l'on peut rencontrer le nombre d'or. Il semble parfaitement fasciné par ce nombre, même quand il manipule ses pures propriétés algébriques et trigonométriques, d'une manière un peu embrouillée d'ailleurs car il conserve à la fois

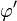
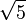
En 1995 l'historienne d'art Marguerite Neveux démonte toutes les études précédentes qui prenaient parti pour le nombre d'or, dans son ouvrage Nombre d'or - radiographie d'un mythe, fruit de 10 ans de recherches.
Rudolf Wittkower est également de son avis, et dit notamment qu'" il est probablement exact de dire qu'aucun architecte de la Renaissance n'a usé des proportions irrationnelles ".
Enfin, on ne compte plus les revues, magazines, livres, sites personnels… parus pour réaffirmer la véracité du mythe, et dans une moindre mesure, ceux édités pour en étudier l’authenticité d’un point de vue bien plus critique. Il reste à noter que bien souvent, l’argumentation des sources trop peu sérieuses est trop mince et affirme par exemple couramment sans démonstration que le nombre d’or a été trouvé dans un temple de la mer des Bahamas, dans la Grande Pyramide, dans les cathédrales, dans les tableaux de Léonard de Vinci, cependant il serait regrettable de ne pas étudier au cas par cas ces exemples et de les réfuter en bloc.
Bref, l'utilisation consciente ou inconsciente dans l’art du nombre d'or reste un sujet hautement polémique.
Nombre d'or et architecture
Quoi qu'on puisse penser de l'intérêt réel du nombre d'or en tant que tel en matière d'esthétique, il est clair qu'un consensus entre les architectes sur une proportion ou une autre — et donc pourquoi pas celle-là — ne pouvait que donner à un ensemble de bâtiments ayant des concepteurs différents un début d'harmonie commune. En ce sens, son rôle principal aurait concerné des questions d'urbanisme plus que d'architecture.
Toutefois, l'intérêt architectural de ce nombre est, que si vous ajoutez, ou bien soustrayez, un carré à un rectangle au nombre d'or, vous retrouvez un rectangle au nombre d'or, ce qui simplifie le travail pour composer une façade suivant des tracés régulateurs. De plus, cette relation complémentaire entre le carré et le rectangle d'or donne une impression de grande stabilité visuelle. Cependant, Marguerite Neveux rejette de tels hypothétiques tracés régulateurs.
L'architecte et urbaniste Le Corbusier lui consacre un essai en créant le Modulor. Il baptise ainsi ce système qu'il rêve de substituer au système métrique et qu'il utilisera dorénavant dans tous ses projets, comme la Cité radieuse de Marseille. C'est de très loin l'utilisation la plus clairement établie du nombre d'or, puisque Le Corbusier en a parlé sans ambiguïté.
Nombre d'or dans la nature
Certains affirment observer le nombre d'or dans l'implantation des feuilles sur la tige des plantes, ou des écailles dans la pomme de pin, ou d'une fleur de tournesol. La présence de la suite de Fibonacci pour ce type de croissance pourrait en effet expliquer ce phénomène.
En revanche, contrairement à une croyance encore tenace, on ne la trouve absolument pas dans la coquille du nautile. En effet, si la spirale du nautile semble bien de forme logarithmique (ce qui se conçoit bien comme première approximation d'une croissance), le rapport est en revanche "seulement" de 1,3 ce qui est bien trop éloigné du nombre d'or. De plus, aucun raisonnement scientifique ne permet jusqu'à présent de prouver ou justifier la présence du nombre d'or.
Certains pensent le découvrir dans la spirale d'ADN, dans la forme d'un œuf, dans les quasi-cristaux ... Vaste domaine de recherche.
Nombres d’or en astronomie
En astronomie, on appelle nombre d’or, le rang d’une année dans le cycle de Méton qui comporte 19 années et permet de faire coïncider à quelques heures près cycles lunaires et cycles solaires. Il existe alors 19 nombres d’or (de 1 à 19) et chaque année possède son nombre d’or. Mais ces nombres d’or n’ont aucun rapport avec le nombre φ étudié précédemment.
On le calcule ainsi :
- diviser l’année par 19 (par exemple pour 2007, 2007 / 19 ≈ 105,6 que l’on tronque à 105) ;
- prendre le reste de la division précédente (105 × 19 = 1995 au lieu de 2007, il reste donc 12 années) ;
- ajouter 1 (12 + 1 = 13) : l’année 2007 a donc pour nombre d’or 13.
Cette règle restera valable tant que le cycle métonique de 19 ans (légèrement trop long d’un peu moins d’une heure et demie) ne sera pas corrigé pour tenir compte de l’avance de ce cycle de près d’un jour au bout d’un peu plus de 16 cycles (soit 310 ans selon les observations actuelles du cycle lunaire). Certains ont proposé de ne pas toucher à ce cycle métonique traditionnel ou au calcul du nombre d’or lui-même, mais d’introduire plutôt un autre cycle apportant les jours supplémentaires de correction des lunaisons à appliquer à un ensemble donné de 16 cycles ; d'autres défendent la modification de la formule du nombre d’or.
Voir aussi le calendrier lunaire perpétuel ou le calcul de la date de Pâques pour connaître son contexte.
Le Cycle de Méton, découvert par l'astronome du même nom, a été révélé en 453 av JC lors des Jeux Olympiques, et les Athéniens, conscients de l'importance d'une telle découverte pour améliorer le calendrier de l'époque, ont fait graver ce cycle en lettres d'or sur un temple dédié à Minerve. C'est de là que vient l'expression nombre d'or pour désigner le rang d'une année dans le cycle de Méton, et par extension, le cycle lui-même. [1]
Bibliographie
- Nombre d'or - radiographie d'un mythe de Marguerite Neveux.
- LE MODULOR, essai sur une mesure harmonique à l'échelle humaine applicable universellement à l'Architecture et à la mécanique de Le Corbusier (Editions de l'Architecture d'Aujourd'hui, collection ASCORAL - 1949)
Notes et références de l'article
- ↑ Que sais-je N°1530, le nombre d'or, par Marius Cleyet-Michaud