Géode - Définition

La construction des coupoles géodésiques a été particulièrement développée par l'architecte américain Richard Buckminster Fuller. L'une de ses géodes les plus remarquables est un dôme (lien) géodésique transparent de 80 m de diamètre qui fut construit sur l'île Sainte-Hélène à Montréal en 1967 pour être le pavillon des États-Unis à l'exposition universelle de Montréal et qui abrite aujourd'hui la Biosphère.

Présentation rapide

Géode par triangulation

La plupart des géodes sont bâties sur le principe suivant : on part d'un icosaèdre.

Il faut noter que chacun des sommets de l'icosaèdre est commun à cinq facettes triangulaires, adjacentes deux à deux, et que cinq arêtes (côtés des facettes) partent de chacun de ces sommets.

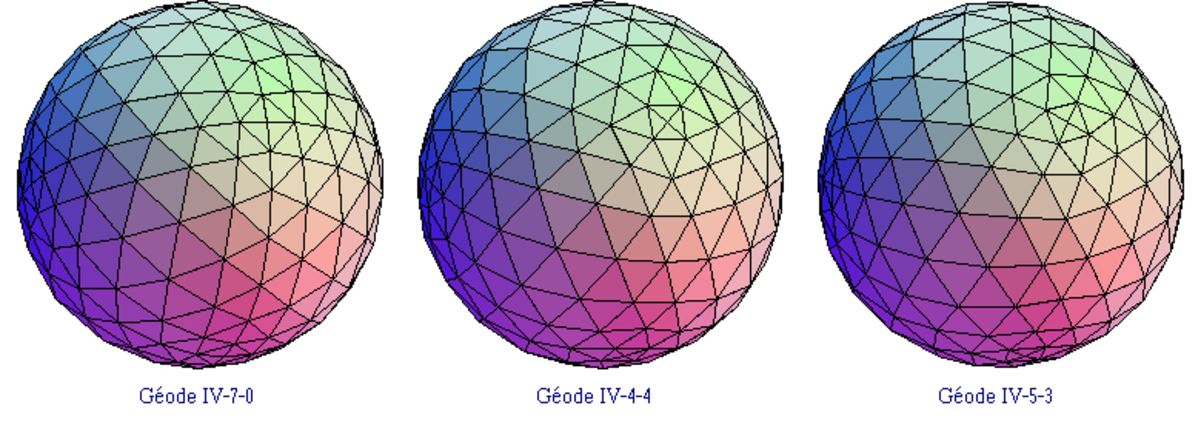
Chaque facette de l'icosaèdre est un triangle équilatéral, que l'on va subdiviser en triangles plus petits qui sont ensuite déformés (par projection radiale) pour être amenés sur la sphère circonscrite à l'icosaèdre. Voici trois exemples de géodes, correspondant chacun à une subdivision différente :

Dans le premier exemple, on a divisé les arêtes des faces de l'icosaèdre en deux segments. Dans le second, les arêtes ont été divisées en trois. Enfin, dans le dernier, elles ont été divisées en dix segments. C'est d'ailleurs sur ce dernier modèle qu'est bâtie la Géode de la Cité des sciences et de l'industrie de la Villette.

Pour repérer l'emplacement des sommets de l'icosaèdre initial, il suffit de trouver les endroits où 5 petits triangles (au lieu de 6) partagent un même sommet !

Géode en nid d'abeille

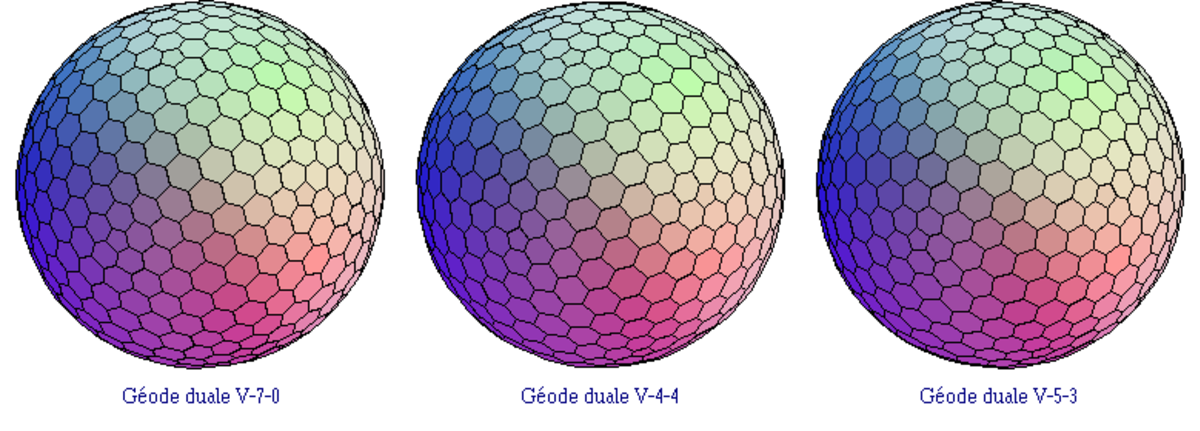
On peut également concevoir des géodes en nid d'abeille en prenant le polyèdre dual des géodes obtenues par triangulation.

Dans la figure ci-dessus (qui est la figure agrandie du polyèdre dual de la géode du dernier exemple précédent basé sur une subdivision en 10 segments), la sphère semble pavée d'hexagones. Mais une observation attentive permet de découvrir que parmi ces hexagones se cachent en fait douze pentagones correspondant aux sommets de l'icosaèdre initial. Il est en effet impossible de recouvrir une sphère en n'utilisant que des hexagones, comme le montre la relation d'Euler entre nombres de faces, d'arêtes et de sommets d'un polyèdre, quel qu'il soit.
Sur la figure, trois de ces 12 pentagones sont bien visibles, un quatrième, peu visible, se trouve près du bord de la figure, dans la direction " onze heures " (que marquerait la grande aiguille d'une montre), enfin un cinquième se cache sur le rebord de la figure, à " trois heures et demie " !

Principes de la construction géométrique d'une géode

Les dômes géodésiques sont des structures basées sur la division (partition) des faces d'un polyèdre régulier dont les faces sont constituées de triangles équilatéraux.

Il n'existe que 3 types de polyèdres réguliers possédant de telles faces équilatérales : le tétraèdre régulier (N = 3), l'octaèdre régulier (N = 4) et l'icosaèdre régulier (N = 5), la notation N utilisée ici représentant le nombre de faces (et aussi le nombre d'arêtes) qui partagent un même sommet.

La division des faces est définie par deux paramètres entiers a et b, positifs ou nuls.

Le premier paramètre a doit être strictement positif.

Le second paramètre b peut être nul mais ne doit pas être supérieur à a.

Une fois choisies les valeurs de N puis de a et de b, la construction du dôme correspondant, que par la suite nous noterons " Géode M-a-b " (notation où le M doit être remplacé par III, IV ou V, selon la valeur en chiffres romains du nombre N), se déroule en 6 étapes, que nous allons expliquer en détail en privilégiant le cas N = 5 (qui correspond à l'immense majorité des géodes) et en l'illustrant dans les 3 cas suivants : , puis et enfin

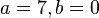
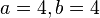
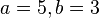
Remarque : les figures qui précèdent correspondent, en utilisant la notation expliquée ci-dessus, aux géodes suivantes :

• dans l'introduction : la géode V-3-1 et sa duale (en rotation)
• au paragraphe 1.1 : la géode V-1-0 (icosaèdre) puis les géodes V-2-0, V-3-0 et V-10-0
• au paragraphe 1.2 : la géode V-10-0 duale

À partir d'un icosaèdre régulier

Étape n° 1

On construit un polyèdre régulier (R) correspondant à la valeur de N

Étape n° 2

• On choisit l'une des faces du polyèdre (R) puis l'une des arêtes de cette face (qui est toujours un triangle équilatéral). Soit AB l'arête choisie et C le sommet opposé à cette arête sur la face choisie.
• On divise alors le segment AB en (a + b) segments de longueur égale et l'on numérote tous les points ainsi définis : le point A reçoit le n° 0, le point suivant le n° 1, le suivant le n° 2, etc. et le dernier, c'est-à-dire le point B, le n° a + b. Soient les points ainsi obtenus.
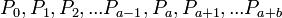
• On trace ensuite le segment .
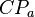
• Enfin, on trace tous les segments parallèles à et passant par chacun des points , sans toutefois dépasser les limites de la face ABC.

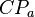
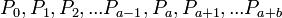
Étape n° 3

• On répète la même opération en changeant respectivement l'arête AB et le sommet C, en BC et A, puis en CA et B ; on obtient ainsi un triple réseau de segments parallèles et équidistants faisant entre eux des angles de 60° et délimitant donc des petits triangles équilatéraux dont certains (sauf si le paramètre b vaut 0) sont incomplets. Ce sont les sommets de ces petits triangles qui vont servir à construire le dôme géodésique, y compris ceux qui sont situés juste à cheval sur l'une des arêtes de la face ABC.
• Bien entendu, il faut répéter les opérations décrites aux étapes 2 et 3 pour toutes les faces du polyèdre (R). Rappelons que le tétraèdre possède 4 faces, l'octaèdre 8 faces et l'icosaèdre 20 faces.

Étape n° 4

• Soit O le centre de la sphère (S) circonscrite au polyèdre (R). Par la projection radiale de centre O, on projette sur la sphère (S) l'ensemble des réseaux obtenus ou, plus exactement, les sommets des petits triangles équilatéraux qu'aux étapes n° 2 et 3, on a obtenus sur chacune des faces de (R).

Étape n° 5

• Pour former les arêtes du dôme géodésique V-a-b, on doit relier les divers sommets obtenus à l’étape précédente : toutefois, il ne faut relier entre eux que les sommets qui sont la projection de sommets appartenant à un même petit triangle équilatéral (voir étape n° 3).

Étape n° 6

Les arêtes obtenues à l'étape précédente forment des triangles sphériques, qui sont la projection radiale des petits triangles équilatéraux résultant de la division des faces du polyèdre initial (R).

• Pour achever le tracé de la géode V-a-b, il suffit d'effacer la trace de toutes les opérations effectuées aux étapes n° 1 à 4 : les sommets des triangles sphériques restants sont les sommets de la géode ; ces sommets, reliés deux à deux, dessinent l'ensemble des sommets et des faces de la géode V-a-b.

• Si au lieu de la géode normale, on souhaite construire la géode duale correspondante, il faut déterminer sur la sphère (S) le centre de chacun de ces triangles sphériques (qui sont donc " en face " des centres des faces de la géode V-a-b normale,) et si les points-centres ainsi obtenus correspondent à des faces adjacentes de la géode normale, on doit joindre ces points deux à deux pour former les arêtes de la géode duale. L'ensemble de ces arêtes dessinent des polygones qui sont les faces de la géode duale ; ces faces sont des hexagones, sauf douze d'entre elles qui sont des pentagones réguliers dont les centres sont situés " en face " des douze sommets du polyèdre générateur (R).

Il faut bien sûr effacer le tracé de la géode normale quand on a fini de tracer les arêtes de la géode duale.

À partir d'un octaèdre régulier

Si l'on choisit comme polyèdre de départ (R) un octaèdre régulier (correspondant pour N à la valeur 4).

la construction exposée ci-dessus conduit à l'étape n° 6 aux résultats suivants :

À partir d'un tétraèdre régulier

Si l'on choisit enfin comme polyèdre de départ (R) un tétraèdre régulier (correspondant pour N à la valeur 3).

la même construction conduit à l'étape n° 6 aux résultats suivants :

Quelques remarques géométriques

Lorsque le paramètre b est nul ou égal au paramètre a, la géode (normale ou duale) possède toutes les propriétés de symétrie de son polyèdre générateur ; par exemple, pour l'icosaèdre : 15 plans de symétrie (passant par deux arêtes opposées), 10 rotations d'ordre 3 (rotation de 120° autour d'un axe passant par le centre de l'une des 20 faces) et 6 rotations d'ordre 5 (rotation de 72° autour d'un axe passant par deux sommets opposés)

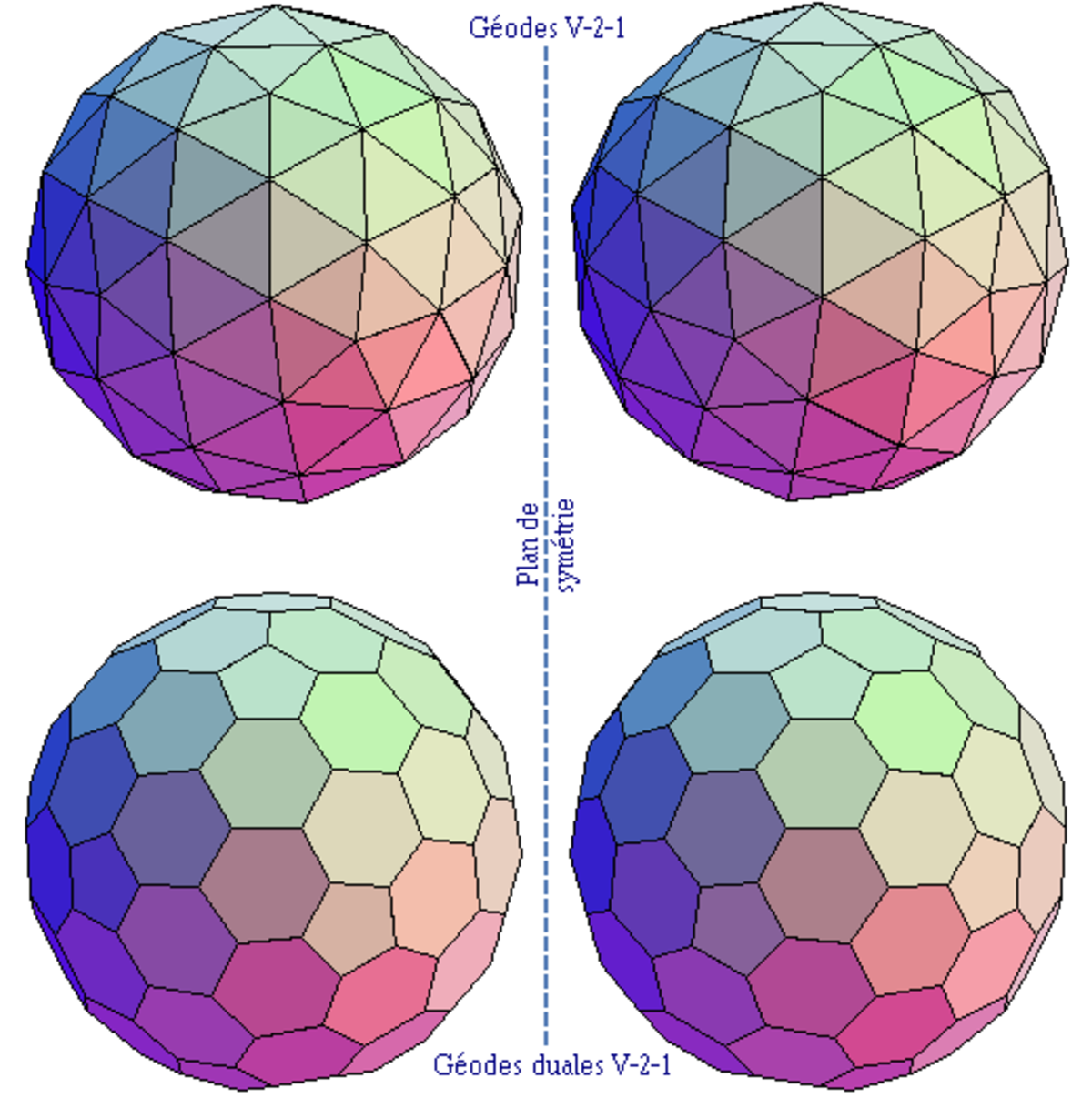
En revanche, lorsque les paramètres a et b sont différents et tous deux positifs, la géode perd ses plans de symétrie et il existe donc deux formes de géodes de type N-a-b, qui sont énantiomorphes (c'est-à-dire symétriques l'une de l'autre dans un miroir, sans être superposables) ; pour s'en convaincre, il suffit de permuter les lettres A et B dans les explications données ci-dessus aux étapes n° 2 et 3 et d'examiner attentivement les figures correspondantes (dans le cas V-5-3) ou la figure ci-dessous :

• les triangles sphériques obtenus à l'étape n° 5 paraissent être équilatéraux (du moins quand le polyèdre générateur est un icosaèdre) mais ils ne le sont pas (leurs angles ne sont jamais tous égaux) et leurs longueurs ne le sont que dans quelques rares cas particuliers ;
• de même, les hexagones obtenus dans la construction des géodes duales paraissent être réguliers mais ils ne le sont généralement pas (toutefois ils le sont lorsque a = b = 1, quel que soit N !) ;
• selon une conjecture émise par Joseph D. Clinton mais qui reste à démontrer, il serait possible de déplacer légèrement les sommets du réseau triangulé décrit aux étapes n° 2 et 3 de façon que les arêtes des dômes N-a-b duaux soient toutes de longueurs égales. J. D. Clinton base sa conviction sur le fait que l'on a découvert l'existence de tels dômes " régularisés " pour toutes les combinaisons de a et de b suivantes :

a + b < 4

a = 4 et b = 0

a = 2 et b = 2

a = 5 et b = 0

et enfin<

a = 3 et b = 3

avec N quelconque (égal à 3, 4 ou 5).
On pourra consulter à ce sujet le document pdf référencé ici.

Si l'on choisit et , la géode V-1-0 normale obtenue est identique au polyèdre (R) générateur de départ. Quant à la géode V-1-0 duale, c'est le polyèdre régulier dual du même polyèdre  ; c'est donc, selon la valeur de N, un dodécaèdre régulier (si ), un cube (si ) ou un tétraèdre régulier (si ).

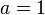
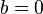
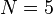
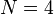
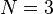
La quantité que l'on convient d'appeler la " densité " d'une géode est intéressante car elle correspond au rapport de la surface des faces triangulaires du polyèdre (R) à la surface des petits triangles obtenus dans la division des faces. Elle intervient notamment dans le formulaire qui donne, en fonction de N, a et b, le nombre de faces F, d'arêtes A et de sommets S des dômes géodésiques normaux et duals.

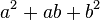
Les arêtes d'un dôme géodésique normal (G) forment une triangulation de Delaunay de l'ensemble de ses sommets ; en outre, le dôme géodésique dual du même dôme (G) constitue une partition de la sphère (S) mais il ne correspond pas rigoureusement au diagramme de Voronoï des sommets du dôme (G), notamment pour les faibles valeurs de la densité .

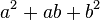
Il n'est pas mathématiquement illogique de s'intéresser encore à un autre type de dômes géodésiques, ceux que l'on pourrait obtenir à partir d'une division (partition) des faces d'un autre polyèdre régulier, le cube ; cette division consisterait à découper chacune des six faces carrées du cube en mini-carrés. Pour construire de tels dômes " quadrangulés ", il suffirait, à l'étape 2 décrite ci-dessus, de diviser l'une des deux diagonales BD d'une face ABCD (carrée) du cube en segments de longueur égale, puis de relier le sommet C au point et enfin de tracer tous les segments parallèles à CP_a et passant par les points , de la diagonale, sans dépasser les limites de la face carrée ABCD, puis, passant à l'étape 3, de faire une construction analogue avec la diagonale AC et le sommet B, et enfin de reproduire le quadrillage ainsi obtenu sur chacune des 5 autres faces du cube. Pour ces dômes, la " densité ", rapport de la surface des faces du cube à la surface des petits carrés obtenus dans la division des faces, vaudrait  ! 

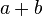
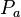
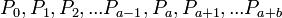
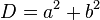
Nota : le formulaire qui suit n'inclut pas le cas particulier des géodes " quadrangulées "

Formulaire

Pour calculer les nombres F, A et S représentant les nombres de faces, d'arêtes et de sommets d'un dôme géodésique de paramètres N, a et b, il faut commencer par calculer les nombres f et D (qui représentent respectivement le nombre de faces du polyèdre régulier générateur (R) et la " densité " de la division des faces de ce polyèdre) à l'aide des deux formules préliminaires suivantes :

   et  

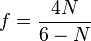
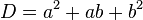
On peut ensuite calculer :

• dans le cas des dômes géodésiques " normaux " :

, 

  et 

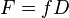
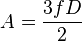
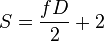
• dans le cas des dômes géodésiques " duals " :

 ,  

   et 

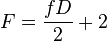
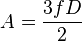
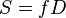
Détails complémentaires :

• les faces des dômes normaux sont toutes d'ordre 3 (ce sont des triangles) tandis que leurs sommets sont de deux types : ceux d'ordre 6 (auxquels aboutissent 6 arêtes) et ceux d'ordre N. Leurs nombres respectifs valent :

   et 

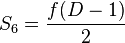
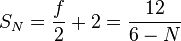
• les sommets des dômes duals sont tous d'ordre 3 (3 arêtes y aboutissent) tandis que leurs faces sont de deux types : celles d'ordre 6 (hexagones) et celles d'ordre N (polygones à N côtés). Leurs nombres respectifs valent :

   et 

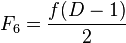
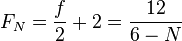
• la droite portant le segement fait avec la hauteur relative au côté AB de la face ABC du polyèdre régulier (R) un angle dont le sinus et la tangente valent respectivement :

   et  

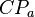
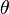
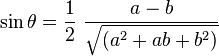
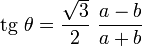
Géodes et architecture

Quelque 300 000 géodes ont été construites à travers le monde. Elles peuvent servir à de très nombreux usages : lieux publics (musées, lieux d'exposition, salles de spectacle, lieux de compétition sportive ou d'entraînement…), centres commerciaux, structures provisoires (forums, expositions, salons, tentes collectives ou individuelles…), habitations collectives (expéditions scientifiques…), structures à usage technique, abris divers (entrepôts, hangars, garages, couverture de réservoirs, abris de jardin), et même habitations privées (bien que cet usage présente de sérieux (en) inconvénients)…

Généralement, le polyèdre générateur est un icosaèdre orienté de telle sorte que l'un de ses 12 sommets (ou le centre de l'une de ses 20 faces) se trouve au point le plus haut de l'édifice. Ceci présente un intérêt non seulement esthétique, mais aussi pratique pendant la phase de construction de la structure (un mât central vertical permettant de soulever l'ouvrage, au fur et à mesure que de nouveaux éléments lui sont ajoutés).

Il est exceptionnel qu'une géode soit complète : le plus souvent, on n'en construit que la partie supérieure et il est d'usage d'indiquer par une fraction simple (et donc approximative) le rapport entre la hauteur de la structure et le diamètre de la sphère circonscrite au polyèdre générateur.

En toute rigueur, on devrait appeler " sphère géodésique " les géodes complètes, et réserver la dénomination de " dôme géodésique " ou " coupole géodésique " aux géodes incomplètes.

Géodes renforcées

Quand une géode est de grandes dimensions, il peut être intéressant, au point de vue architectural, d'en renforcer la cohésion en superposant deux coupoles géodésiques, duales l'une de l'autre. Il y a deux façons de réaliser ce renforcement :

• on peut placer une géode normale " à l'extérieur " du bâtiment et la doubler " à l'intérieur " d'une géode duale, ou au contraire
• on peut placer une géode normale " à l'intérieur " du bâtiment et la doubler " à l'extérieur " d'une géode duale, ce qui est généralement considéré comme plus satisfaisant au plan esthétique.

Le principe de ce renforcement consiste :

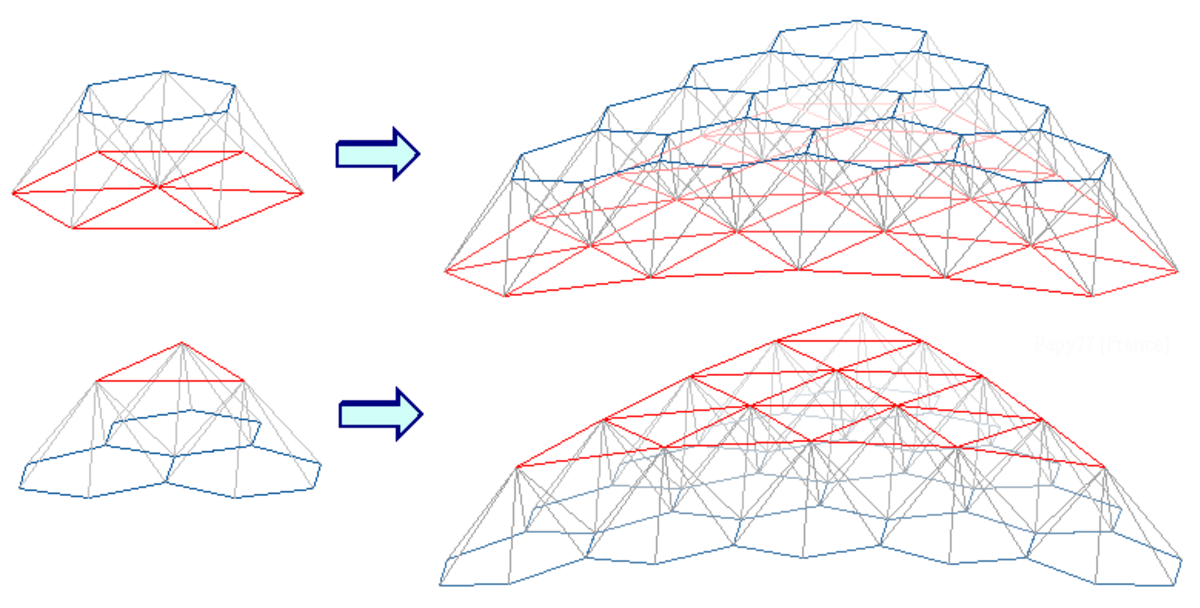
• à prendre un groupe de 6 faces triangles (d'une géode normale) ayant un sommet commun et de bâtir sur la base de chacun de ces 6 triangles une pyramide (à 6 faces) dont le sommet, situé à l'aplomb du centre du triangle, est relié à chaque sommet du triangle servant de base par des arêtes dont la longueur est proche de la moyenne des longueurs des arêtes de la géode normale ; on relie ensuite les sommets de ces 6 pyramides de façon à former un hexagone qui constitue l'une des faces de la géode duale qui double la géode normale ; ou encore, mais cela revient au même, le renforcement consiste :
• à prendre un groupe de 3 faces hexagonales (d'une géode duale) ayant un sommet commun et de bâtir sur la base de chacun de ces 3 hexagones une pyramide (à 12 faces) dont le sommet, situé à l'aplomb du centre de l'hexagone, est relié à chaque sommet de l'hexagone servant de base par des arêtes dont la longueur est proche de la moyenne des distances entre les centres des faces adjacentes de la géode duale ; on relie ensuite les sommets de ces 3 pyramides de façon à former un triangle qui constitue l'une des faces de la géode normale qui est ainsi doublée par la géode duale.

Le schéma ci-dessus montre, dans sa partie supérieure, une géode normale intérieure doublée d'une géode duale extérieure, et dans sa partie inférieure, une géode normale extérieure doublée d'une géode duale intérieure.

Remarques diverses

Dans la typologie qu'il a établie, l'architecte américain Richard B. Füller qui a mis en évidence l'intérêt des dômes géodésiques pour la construction de grandes structures en forme de coupole, nomme " fréquence " d'une géode la quantité a + b.

Il distingue 3 classes de dômes géodésiques : les dômes les plus simples (avec b = 0) correspondent à la classe I (ils sont dits " triacon "), ceux de la classe II correspondent aux cas où a = b (ils sont dits " alternate "), et enfin la classe III englobe tous les dômes dits " twisted " (c'est-à-dire tournants ou tors en français) pour lesquels b n'est ni nul ni égal à a. Mais selon d'autres sources (ou auteurs), les classes I et II correspondraient respectivement aux cas a = b (" alternate ") et b = 0 (" triacon ")

Certains auteurs contestent que Fuller soit l'inventeur des dômes géodésiques et justifient leur point de vue en rappelant que dès 1922, l'ingénieur Walter Bauersfeld, travaillant chez Zeiss, a eu l'idée d'une structure de type V-1-1 duale pour la construction, à Iena, du premier planétarium ouvert au public. Toutefois, il semble bien que Bauersfeld n'ait vu dans cette idée que la solution d'un problème optique et qu'il n'ait pas entrevu la possibilité d'une généralisation de cette idée à la construction de vastes bâtiments à usage général.

Il semble qu'aucun dôme géodésique de classe III et de grandes dimensions n'ait été réalisé par un architecte, probablement parce que la construction en est un peu plus compliquée, sans contrepartie d'ordre esthétique…

De même, aucun dôme géodésique correspondant à N = 3 ou à N = 4 n'a été construit par un architecte ; ceci s'explique aisément par la très grande dispersion des longueurs des arêtes, celle-ci entraînant à la fois une beaucoup plus grande fragilité et une esthétique assez peu agréable, surtout lorsque N = 3 ; ces dômes sont donc de pures curiosités mathématiques !

De même, et pour les mêmes raisons, aucune géode quadrillée (à base de cube) n'a été construite !

Quelques géodes remarquables

Voici, classés par ordre de diamètre décroissant, les dômes géodésiques réputés comme les dix plus grands au monde :

1. Fantasy Entertainment Complex (2 dômes jumeaux) : Île de Kyushu, Japon, 216.4 m (710 pieds) de large, construits en 2002 par Starnet
2. Le Dôme de Nagoya (espace multi-fonctionnel, sport et concerts) : Nagoya, Japon, 187.2 m (614 pieds) de large, construit en 1997 par Takenaka Corporation
3. Tacoma Dome (espace multi-fonctionnel) : Tacoma (Washington-WA, USA), 161.5 m (530 pieds) de large, en bois, construit en 1983 par Western Wood
4. Superior Dome (Dôme supérieur), Northern Michigan University : Marquette (Michigan-MI, USA), 160 m (525 pieds) de large, dôme en bois construit en 1991 par Western Wood
5. J. Lawrence Walkup Skydome (Multi-Purpose Arena), Northern Arizona University : Flagstaff (Arizona-AZ, USA), 153 m (502 pieds) de diamètre, dôme en bois construit en 1977 construit par Western Wood
6. Round Valley Ensphere (stade multi-sports), High School High School : Springerville (Arizona-AZ, USA), 134.1 m (440 pieds) de large
7. Carnival Cruise Ship Terminal (anciennement Spruce Goose Hangar) : Long Beach (California-CA, USA), 126.5 m (415 pieds) de diamètre, construit en 1982 par Temcor
8. Formosa Plastics Storage Facility (10 dômes-hangars identiques dont 9 sont utilisés pour le stockage du charbon et un pour celui du sel ; un onzième dôme identique a été ajouté en 2002 pour doubler les capacités de stockage de sel) : Mai Liao, Taiwan, 122.5 (402 pieds) de large, en aluminium, construit par Temcor
9. Union Tank Car Maintenance Facility : Baton Rouge (Louisiane-LA, USA), 117 m (384 pieds) de large, construit en 1958 par Robert Buckminster Fuller et Synergetics Inc.
10. Lehigh Portland Cement Storage Facility : Union Bridge (Maryland-MD, USA), 114 m (374 pieds) de large, en aluminium, construit en 2001 par Temcor.

Autres dômes géodésiques remarquables :

1. Spaceship Earth dans EPCOT à Walt Disney World Resort (50 m de diamètre suréléve de 5 m au-dessus du sol) l'une des rares sphères géodésiques construites.
2. La Biosphère de Montréal.

En France, on peut recenser un certain nombre de dômes géodésiques, en commençant par les plus connus :

1. La Géode, Cité des sciences et de l'industrie, à la Villette, 36 m de diamètre, construite par l'architecte Adrien Fainsilber et l'ingénieur Gérard Chamaillou en 1985, et dont les facettes triangulaires, non planes, sont des triangles sphériques réfléchissants !
2. Le Palais des sports, Paris, 61 m de large, construit en 1959 par Pierre Dufau, Porte de Versailles, à côté du Parc des expositions, et rénové en 2002
3. Le Radôme de la " Signals Intelligence Station ", à Kourou, en Guyane française
4. La Géode de l'IUT d'Agen, construite par le Cabinet Triangle - Boussac
5. Le dôme du Laboratoire de Mécanique et Génie Civil à l'Université des Sciences et Techniques du Languedoc à Montpellier, 10 m de diamètre
6. Un réservoir pétrochimique, construit par Vacono.

Autres exemples de structures géode

Une géode V-1-1 duale a exactement la structure des ballons de football en usage dans les compétations officielles : sur ces ballons, les 12 pentagones sont teints en noir tandis que les 20 hexagones sont teints en blanc.

Les balles de golf sont creusées de petits alvéoles dont le nombre, la forme et la position peuvent améliorer les performances des joueurs ; parmi les balles de golf professionnelles, on rencontre fréquemment des balles dont la disposition des alvéoles circulaires reproduit celle des faces (hexagones et pentagones) d'une géode V-6-0 duale.

Certains composés organiques remarquables tels que les C₆₀ dont la structure est proche des géodes V-1-1 ont été baptisés fullerènes en hommage à R. B. Fuller ; on les appelle aussi parfois " footballènes ".

Virus

La majorité des virus sont des " virus icosaédraux " (en anglais " icosahedral viruses ") ou plus exactement des " virus à nucléocapside icosaédrale " : leur particularité tient à leur structure qui, très proche de celle d'un dôme géodésique, normal ou dual (sans toutefois la projection radiale sur la sphère (S)), leur confère une grande stabilité. Ils correspondent toujours à N = 5 et le plus souvent à des valeurs faibles de a et de b.

Parmi ces nombreux virus, on peut citer ceux des hépatites A, B, C et E, celui de la poliomyélite, celui du sida (HIV-1), celui de la fièvre jaune, celui de la variole, celui de la fièvre aphteuse, le virus habituel de la bronchiolite (VRS), ceux des verrues communes et plantaires (Papillomavirus HPV-3 et HPV-1), celui de la rubéole ou encore celui du " rhume de cerveau " ; mentionnons aussi le groupe des 8 virus dits herpesviridae qui possèdent tous la structure V-5-0 et qui peuvent induire différentes maladies humaines : varicelle, zona, mononucléose infectieuse, herpès labial, herpès néonatal et MST telles que l'herpès génital simple et l'herpès à cytomégalovirus.

Certains de ces virus sont " twisted " et correspondent donc à la classe III de Fuller : par exemple le Polyomavirus et le Papillomavirus qui sont du type V-2-1. On connaît même un virus de type V-10-7 (celui qui infeste l'algue Phaeocystis pouchetii).

Symbolique

les trois polyèdres réguliers dont les faces sont des triangles équilatéraux correspondent pour Platon aux éléments feu, air et eau. Plus précisément, dans son Timée, Platon, évoquant la façon dont le Créateur a façonné l'Univers, fait correspondre le tétraèdre au feu, l'octaèdre à l'air et l'icosaèdre à l'eau (le cube étant associé à la terre).