Réaction nucléaire - Définition

Une réaction nucléaire est une transformation d'un ou plusieurs noyaux atomiques, elle se distingue d'une réaction chimique qui concerne les électrons ou les liaisons entre les atomes. Dans une réaction nucléaire, deux noyaux atomiques entrent en collision et produisent des produits différents des particules originelles. En principe, plus de deux particules pourraient entrer en collision, mais cela c'est beaucoup moins probable. Dans le cas de la radioactivité, la transformation est spontanée, mais dans le cas d'une réaction nucléaire, elle est produite par une particule mouvante. Si les particules se séparent après la collision sans être transformées, le processus n'est pas une réaction, mais une collision élastique.

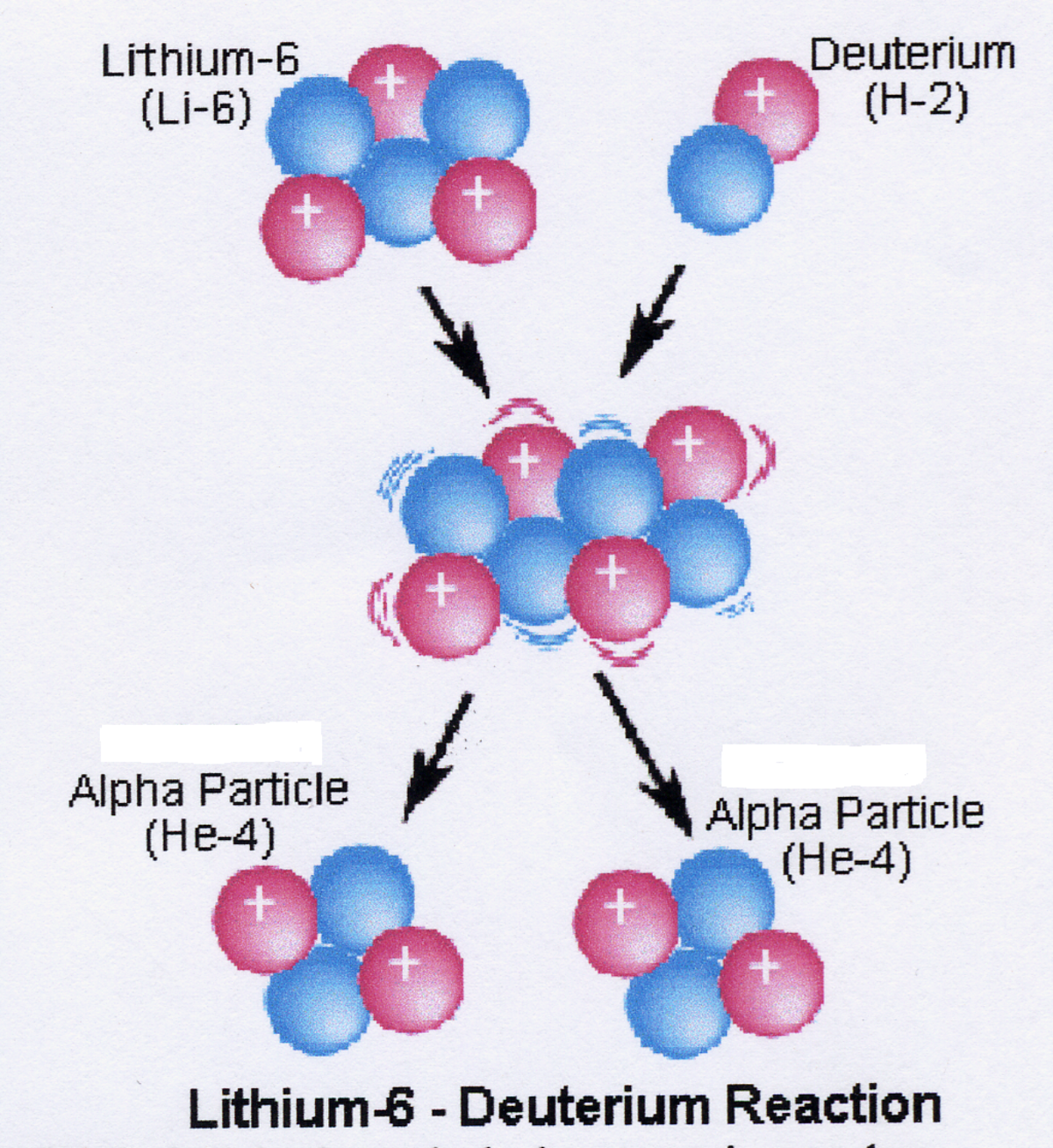
Dans l'exemple de réaction montré à droite, ⁶Li and deuterium réagissent en formant un noyau atomique intermédiaire très excité ⁸Be qui se désintégre très vite en produisant deux particules alpha. Ici, les protons sont représentés par des sphères rouges, et les neutrons, par des sphères bleues.

Représentation

Une réaction nucléaire peut être représentée par une équation semblable à celle représentant une réaction chimique. Des désintégrations nucléaires peuvent être représentées d'une manière semblable, mais avec seulement un noyau à gauche.

Chaque particule est écrite avec son symbole chimique, avec son numéro atomique à gauche en bas, et son nombre de masse en haut. Pour le neutron, le symbole est n. Le proton peut être écrit "H" (noyau d'hydrogène) ou "p".

Pour vérifier l'équation, on doit contrôler que les sommes des nombres atomiques soient égales à gauche et à droite (à cause de la loi de conservation de la charge électrique, et que les sommes des nombres de masse soient aussi égales à gauche et à droite (à cause de la loi de conservation du nombre baryonique. Par exemple:

₃⁶Li + ₁²H → ₂⁴He + ₂⁴He

Évidemment, l'équation est correcte. Elle pourrait aussi être écrite

₃⁶Li + ₁²H → 2 ₂⁴He

Représentation simplifiée

Si quelques particules paraissent très souvent, on utilise des abréviations. Par exemple, le noyau ⁴He (qui s'appelle aussi particule alpha) est abrégé avec la lettre grecque "α". Les deuterons (hydrogène lourd, ²H) sont dénotés simplement "d". Aussi, comme les nombres atomiques sont donnés implicitement par les symboles chimiques, ils peuvent être supprimés quand l'équation a été vérifiée. Finalement, dans beaucoup de réactions, un noyau relativement lourd est frappé par une particule légère d'un petit groupe de particules communes, émettant une autre particule commune, et produisant un autre noyau. Pour ces réactions, la notation peut être beaucoup simplifiée de la manière suivante:

( particule d'entrée, particule de sortie )

Par conséquent, on pourrait périphraser l'exemple précédant en introduisant des symboles:

₃⁶Li + d → α + α

puis, supprimant les nombres atomiques:

⁶Li + d → α + α

et finalement, utilisant la forme condensée:

⁶Li(d,α)α

Conservation d' énergie

Il est possible que de l'énergie cinétique soit libérée pendant une réaction (réaction exothermique), ou que de l'énergie cinétique doit être ajoutée pour rendre possible la réaction (réaction endothermique). Pour décider cette question, il faut une table de masse des particules très exacte (voir http://physics.nist.gov/PhysRefData/Compositions/index.html). D'après cette table, le noyau ₃⁶Li a une masse atomique de 6.015 unités de masse atomique (abrévié u), le deuteron a 2.014 u, et le noyau ₂⁴He a 4.0026 u. Par conséquent:

• Masse de repos totale à gauche = 6.015 + 2.014 = 8.029 u
• Masse de repos totale à droite = 2 × 4.0026 = 8.0052 u
• Perte de masse = 8.029 - 8.0052 = 0.0238 unités de masse atomique.

Dans une réaction nucléaire, l'énergie relativiste totale est conservée. Par conséquent, la masse perdue doit réapparaître comme énergie cinétique. Utilisant la formule d'Einstein E = mc², on peut déterminer la quantité d'énergie libérée.

Mais d'abord, il faut calculer l'énergie équivalente à une unité de masse atomique:

1 u c² = (1.66054 × 10^-27 kg) × (2.99792 × 10⁸ m/s)² 

= 1.49242 × 10^-10 kg (m/s)² = 1.49242 × 10^-10 J (Joule)

× (1 MeV / 1.60218 × 10^-13 J)

= 931.49 MeV,

Par conséquent, 1 u c² = 931.49 MeV.

Alors, la quantité d'énergie cinétique produite est 0.0238 × 931 MeV = 22.4 MeV.

Ou, exprimé d'une manière différente: la masse est réduite par 0.3 %.

C'est une grande quantité d'énergie pour une réaction nucléaire; la quantité est si grande parce que l'énergie de liaison par nucléon du nucléide ⁴He est exceptionnellement large, parce que le noyau de ⁴He est doublement magique. Par conséquent, les particules alpha paraissent souvent au coté droit de l'équation.

L'énergie libérée dans une réaction nucléaire peut apparaître en trois manières différentes:

• énergie cinétique des particules produites
• émission des photons de très grande énergie, appelés rayons gamma
• une partie de l'énergie peut rester dans le noyau, comme niveau métastable.

Si le noyau produit est métastable, cela est indiqué par un astérisque ("*") près de son nombre atomique. Éventuellement, cette énergie est libérée par transmutation nucléaire.

En général, le noyau produit a un numéro atomique différent, et par conséquent, la configuration de ses couches électroniques n'est pas juste. Alors les électrons, en s'arrangeant, émettent aussi des rayons X.

"Q-value"

En écrivant l'équation pour la réaction nucléaire (d'une manière analogue à une équation pour une réaction chimique) on peut ajouter l'énergie de réaction à droite:

Noyau cible + projectile -> Noyau produit + éjectile + Q.

Pour le cas spécial discuté en haut, nous avons déjà calculé l'énergie de réaction: Q = 22.4 MeV. Alors:

₃⁶Li + ₁²H → ₂⁴He + ₂⁴He + 22.4 MeV

L'énergie de réaction ("Q-value" en anglais) est positive pour les réactions exothermiques et négative pour les réactions endothermiques. D'une part, elle est la différence entre les sommes des énergies cinétiques à droite et à gauche. Mais d'autre part, elle est aussi la différence entre les masses de repos nucléaires à gauche et à droite (et de cette manière, nous avons calculé la valeur en haut).

Taux de réaction

Si une réaction est vérifiée quant aux numéros atomiques et nombres de masse (comme montré en haut), cela ne veut pas dire que la réaction peut avoir lieu. Le taux de réaction dépend de l'énergie des particules, du flux des particules et de la section efficace de la réaction.

Comparaison entre neutrons et ions

Dans la collision initiale, les particules doivent s'approcher si près pour que la force nucléaire forte (d'un rayon d'action très réduit) puisse entrer en jeu. Comme les particules nucléaires ont normalement des charges positives, ils doivent surmonter une répulsion électrostatique considérable. Même si le nucléide cible fait partie d'un atome neutre, l'autre particule doit s'approcher du noyau de charge positive. Par conséquent, il faut d'abord accélérer les projectiles à haute énergie, par exemple, par:

• accélérateur de particules
• une température très grande, quelques millions de degrés, produisant des réactions thermonucléaires, comme au centre du soleil (voir plus bas)
• rayons cosmiques

Les neutrons, d'autre part, n'ont pas de charge électrique, et ils peuvent effectuer une réaction nucléaire à des énergies très petites. Fréquemment, la section efficace croît même si l'énergie décroît.

Le Soleil

Le Soleil est un énorme réacteur thermonucléaire auto-entretenu. Pour l'instant, aucune dérive n'est à craindre, cette réaction explosive est contenue par la force gravitationnelle. Regardons ce qui ce passe au sein du Soleil pour comprendre ce qu'est une réaction nucléaire.

• Il existe deux types de réaction, la fission et la fusion, la fission consiste à séparer le noyau de l'atome (séparer les protons et les neutrons entre eux) et la fusion est le fait d'associer deux noyaux pour former un nouveau noyau. Tous les éléments sont formés ainsi : à l'origine de l'Univers, il n'y avait que de l'hydrogène mais les réactions au cœur des étoiles forment tous les autres éléments jusqu'au fer, les éléments plus lourds sont formés par un autre procédé.
• Sachez que la fusion produit beaucoup plus d'énergie (Les premières bombes nucléaires fissionnaient des atomes d'uranium, mais aujourd'hui les bombes nucléaires fusionnent des atomes hydrogène, bombe H, ces bombes sont beaucoup plus puissantes et destructrices).
• Dans notre soleil, du fait des très hautes températures qui y règnent, les particules sont très agitées et possèdent énormément d'énergie cinétique (vitesse). Du fait de la grande vitesse des atomes, les atomes ne peuvent exister sous forme normale car les électrons refusent de 'graviter' autour. (Imaginez que la Terre est le noyau et que la Lune est un électron; si on chauffe la Terre (soyez imaginatif) elle se mettra à vibrer. Plus on chauffe, plus elle vibre fort, ces vibrations deviendront si fortes que la Lune ne pourra plus tourner autour, on dira donc que la Terre est ionisée).
• Bien qu'ils se dirigent les uns vers les autres, les noyaux ne s'entrechoquent pas car la force électromagnétique les repousse (les noyaux sont tous les deux positifs). Mais si on augmente la température, les noyaux gagnent de la vitesse et lors des chocs, ils se rapprochent toujours de plus en plus, jusqu'à ce que les noyaux entrent en contact et que la force nucléaire forte prenne le relais, mais comme elle est des milliers de fois plus puissante que la force électromagnétique, les noyaux se lient entre eux et forment un seul atome.
• La propriété remarquable de cette réaction réside dans le fait que la masse du noyau est légèrement inférieure à la somme des masses des deux protons du début de la réaction. La réaction nucléaire de fusion s'accompagne donc d'une perte de masse.
• Or, Einstein montra par la théorie de la relativité que la masse peut se transformer en énergie et que l'énergie peut se transformer en masse selon la célèbre formule E = MC² qui énonce que l'énergie est égale au produit de la masse par le carré de la vitesse de la lumière. La perte de masse de la réaction citée plus haut correspond à une libération d'énergie. C'est ainsi qu'en transformant une fraction de sa masse que notre Soleil trouve les ressources qui lui sont nécessaires. Cette méthode est beaucoup plus efficace que les réactions chimiques ou la contraction Kelvin-Helmholtz. Elle permet à une étoile comme la nôtre de briller pendant 10 milliards d'années.