Exergie - Définition

En thermodynamique, l'exergie est une fonction d'état très particulière car elle est la somme de 2 fonctions d'état d'unités différentes : F° = U - T° S . Cette fonction a été très étudiée après Duhem (1861-1916) par Gouy (1854-1926).

Un peu tombée en désuétude, malgré son utilisation par Einstein, elle revient " sur le marché ", par le biais ingénieur des réflexions sur le " Gaspi "llage, lors des années 70, suivant le choc pétrolier : en effet , il s'agit de mesurer le degré d'irréversibilité d'une transformation non cyclique dans un environnement de température T°. Cette fonction est aussi appelée énergie disponible ou disponibilité énergétique ( en anglais : availability), car on démontre que sa chute entre un état A et un état B est le travail maximal récupérable : -W < ou = - Δ F° .

Comme cela est peu intuitif, il n'est pas déraisonnable de dire cette phrase de 4 façons possibles :

1. Si l'on chute énergétiquement d'un état A désordonné vers un état B ordonné, il faut payer le prix de l'information gagnée (-T°Δ S), on ne pourra récupérer que moins que - Δ U , et plus précisément -Δ U + (+T°Δ S,négatif hélas!)
2. Si au contraire A est ordonné et B désordonné , ce serait du Gaspi que de récolter seulement - Δ U .Il faut récolter plus :- Δ U + (T°Δ S, boni positif à ne pas manquer)
3. Si l'on monte énergétiquement d'un état A désordonné vers un état ordonné, il va falloir payer le prix fort : non seulement W > ΔU > 0, mais plus encore, W > ΔU + le prix de l'info à payer -T° ΔS, positif
4. Par contre, si l'on monte énergétiquement d'un état ordonné vers un état désordonné,on aura à payer moins que Δ U >0 d'une quantité -T°Δ S, négative.

Il se pourrait même que l'on récupère du travail dans l'opération, si B est très désordonné : voilà qui n'était pas , a priori, intuitif : certaines piles au mercure et calomel réalisent cet apparent prodige.

Dès que l'on a pris conscience que récupérer de l'information chaude coûte cher, tout devient assez raisonnable : prendre l'exemple de la boîte de Maxwell ; on conçoit bien que séparer les billes blanches et noires dans chaque compartiment est d'autant plus difficile que les bords de la boîte sont vibrants à une haute température T°. C'est même très exactement ce prix que l'on doit payer pour séparer de l'hexafluorure d'uranium 235 de son isotope 238 : faire fonctionner " un démon de Maxwell " coûte d'autant plus que les particules vont vite.

Notion de potentiel F°

Bien sûr, si W=0 , le système ne peut évoluer que vers l'état où F° sera minimal ; et il y restera. Oh ! mais voilà qui exige rééducation de l'intuition mécanique usuelle : ce n'est pas l'état d'énergie U minimale qui est l'équilibre.

Ce n'est pas non plus S maximal, car le système peut rétrocéder de l'énergie au thermostat.

En définitive, ni l'un ni l'autre, mais minimum conjoint de U-T°S= F°(T,V).

À volume constant, cela donne U/S à V constant = T°, c'est-à-dire un résultat TRES INTUITIF finalement : T = T°

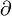
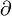
Donc, à l'équilibre monotherme isochore, F°(T, V) = F(T°,V) ( faire très attention à l'écriture); cela justifie qu'en chimie, on utilise pratiquement toujours l'Energie libre F et non pas l'exergie F°.

Exergie monobare

Tout se généralise dans le cas d'un pressostat de pression P°, lors d'une transformation monotherme. Ce qui interviendra est G°(T,P) = U + P°V - T°S, et tous les raisonnements tiennent à condition de parler du travail W* , autre que celui des forces de pression (égal à -P°Δ V)

Stabilité de l'équilibre

La considération de la différence seconde qui doit être positive donne des inégalités intéressantes, dites inégalités de Le Châtelier (ou inégalités de Le Châtelier-Braun)

Bibliographie

• Van Wylen : Thermodynamique
• Kubo : Thermodynamics
• l'Ecole Suisse...
• Callen : Thermodynamics
• Bruhat : Thermodynamique