Deuxième principe de la thermodynamique - Définition

Principes de la thermodynamique
Principe zéro de la thermodynamique
Premier principe de la thermodynamique
Deuxième principe de la thermodynamique
Troisième principe de la thermodynamique

Le deuxième principe de la thermodynamique (également connu sous le nom de deuxième loi de la thermodynamique) établit l'irréversibilité des phénomènes physiques, en particulier lors des échanges thermiques. C'est un principe d'évolution qui fut énoncé pour la première fois par Sadi Carnot en 1824. Il a depuis fait l'objet de nombreuses généralisations et formulations successives Clapeyron (1834), Clausius (1850), Lord Kelvin, Ludwig Boltzmann en 1873, Max Planck (Histoire de la thermodynamique et de la mécanique statistique), tout au long du XIX^e siècle et au-delà.

Énoncé de la loi

Toute transformation d'un système thermodynamique s'effectue avec augmentation du désordre global incluant le désordre du système et le désordre du milieu extérieur. On dit encore qu'il y a création d'entropie car la fonction d'état entropie : S, est une mesure du désordre.

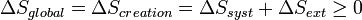
Dans le cas d'une transformation réversible, la création d'entropie est nulle.

Remarques

• L'entropie d'un système isolé ne peut qu'augmenter ou rester constante puisqu'il n'y a pas d'échange de chaleur avec le milieu extérieur.

• L'entropie d'un système peut diminuer mais cela signifie que l'entropie du milieu extérieur augmente de façon plus importante ; le bilan entropique étant positif ou nul si la transformation est réversible.

Le second principe est un principe d'évolution qui stipule que toute transformation réelle s'effectue avec création d'entropie.

Notion de réversibilité

Une transformation réversible est une transformation quasistatique susceptible d'être inversée à la suite d'une modification progressive des contraintes extérieures, en permettant au système de retrouver les états antérieurs successifs. En fait cela revient à passer le film de la transformation à l'envers ! Si ce film paraît ridicule c'est que la transformation n'est pas réversible. En réalité, toutes les transformations réelles sont irréversibles. Une transformation réversible représente en effet, le cas limite d'une transformation réelle, conduite d'une manière infiniment lente, constituée d'une suite d'états d'équilibre infiniment voisins et caractérisée par des phénomènes dissipatifs nuls. C'est donc un modèle idéal de transformation.

On peut recenser plusieurs causes d'irréversibilité (liste non exhaustive) :

• inhomogénéité (source de diffusion) : densité moléculaire, température, pression,...
• phénomène dissipatif : frottements fluides et solides
• réorganisation spontanée de la matière : réaction chimique.

Formulations du second principe

Le second principe introduit la fonction d'état extensive S, appelée entropie. La variation d'entropie d'un système, lors d'une transformation quelconque, peut être décrite comme la somme d'un terme d'échange et d'un terme de création :

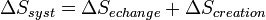
• Le terme de création, toujours positif ou nul, impose le sens de l'évolution de la transformation,  ; l'égalité n'a lieu que pour une transformation réversible.
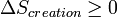
• Le terme d'échange dans le cas d'un système fermé échangeant la quantité de chaleur Q avec le milieu extérieur à la température T est égal à .

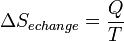
Une autre formulation est possible comme nous l'avons vu précédemment, en considérant l'entropie du système et l'entropie du milieu extérieur. Cette formulation est totalement compatible avec la précédente.

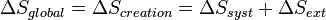
En effet

correspond à l'entropie échangée par le système avec le milieu extérieur. Si l'on se place du côté du milieu extérieur le signe s'inverse et donc:

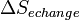
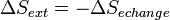
Il s'ensuit

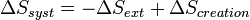
D'où

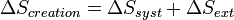
La variation d'entropie globale correspond à l'entropie créée et est égale à la somme des variations d'entropie du système et du milieu extérieur. Elle est toujours positive dans le cas des transformations réelles irréversibles. En revanche dans le cas idéal des transformations réversibles elle est nulle.

Considérons une transformation effectuée soit de façon réversible soit de façon irréversible, à la température T. L'entropie étant une fonction d'état sa variation sera la même pour les deux chemins envisagés. En revanche la chaleur dépendra du chemin suivi car elle n'est pas une fonction d'état.

• Transformation réversible:

puisque l'entropie créée est nulle.

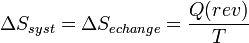
• Transformation irréversible:

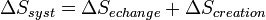
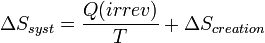
Il s'ensuit que \frac{Q(irrev)}{T}~" > puisque l'entropie créée est positive.

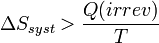
L'expression ainsi obtenue a été formulée par Clausius. On l'appelle encore inégalité de Clausius. C'est une autre façon d'exprimer le second principe.

• Conséquence sur le transfert de chaleur:

Intuitivement on sait que la chaleur passe d'un corps chaud à un corps plus froid. Le second principe permet de le démontrer. Considérons un système isolé constitué de deux sous-systèmes, syst1 et syst2 dont les températures respectives T1 et T2 sont différentes.

La chaleur échangée par syst1 est Q1 et celle échangée par syst2 est Q2. Comme le système est isolé la chaleur échangée avec le milieu extérieur est nulle, donc Q1 + Q2 = 0 . D'où Q2 = - Q1.

Appliquons le second principe

ΔS_créée = ΔS_syst + ΔS_ext > 0

or ΔS_syst = ΔS_syst1 + ΔS_syst2 et ΔS_ext = 0 puisque le système est isolé.

Il s'ensuit :

ΔS_créée = ΔS_syst1 + ΔS_syst2

ΔS_syst1 = Q1/T1

ΔS_syst2 = Q2/T2 = -Q1/T2

Donc ΔS_créée = Q1/T1 - Q1/T2

ΔS_créée = Q1 (1/T1 - 1/T2)

Comme la transformation est irréversible :

ΔS_créée = Q1 (1/T1 - 1/T2) > 0

Si T1 est supérieure à T2, il faut que Q1 soit négative pour que le bilan entropique soit positif. D'après la règle des signes, cela signifie que le syst1 fournit la chaleur au syst2 qui la reçoit et donc que la chaleur passe du chaud au froid.

En toute rigueur, la température ne change pas brutalement entre les deux sous-systèmes car au voisinage de la frontière, la température varie progressivement entre T1 et T2. On dit qu'il y a un gradient de température ; phénomène intimement lié à la notion d'irréversibilité. Néanmoins ce phénomène ne s'oppose pas à la démonstration précédente démontrant le sens du transit de chaleur. Si les températures T1 et T2 sont très proches l'une de l'autre, on peut considérer que la transformation se rapproche d'une transformation réversible (petit déséquilibre de la variable température) et l'on constate alors que ΔS_créée tend vers zéro.

• Conséquence sur le travail utile fourni par un système:

Le travail ainsi que la chaleur ne sont pas des fonctions d'état et leur valeur dépend de la nature de la transformation affectant le système.

Considérons une transformation effectuée soit de façon réversible soit de façon irréversible à la températute T. La variation d'entropie sera la même car l'entropie est une fonction d'état. En revanche, W(rév)≠ W(irrév) et Q(rév)≠ Q(irrév).

ΔS(syst) = Q(rév)/T

ΔS(syst) > Q(irrév)/T

Donc Q(rév) > Q(irrév)

Appliquons maintenant le premier principe

ΔU = W(rév)+ Q(rév) = W(irrév) + Q(irrév)

Il en résulte que : W(rév)< W(irrév)

Or pour un système moteur fournissant du travail, le travail est compté négativement d'après la règle des signes choisie en thermodynamique. Ce qui est important c'est la valeur absolue du travail utile. D'où:

|W(rév)| > |W(irrév)|

Le travail utile fourni par un système moteur est plus important si la transformation est réversible.

Les frottements étant la principale cause d'irréversibilité on comprend pourquoi on essaye de les minimiser par la lubrification.

Historique de la loi

L'origine de la deuxième loi de la thermodynamique remonte à 1824 et est due au physicien français Sadi Carnot, fils de Lazare Carnot. C'est lui qui, dans le traité "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Sadi Carnot utilisait le terme de machine à feu pour désigner les machines thermiques), fut le premier à établir que le rendement d'une telle machine dépendait de la différence de température entre la source chaude et la source froide. Bien qu'utilisant le concept dépassé du calorique qui considérait que la chaleur, par analogie avec un fluide, était une substance matérielle qui pouvait être soit ajoutée, soit enlevée, soit transférée d'un corps à l'autre, il réussit, par une expérience de pensée, à imaginer le principe suivant : le rendement maximum η d'un moteur ditherme fonctionnant avec une source chaude de température T₁ et une source froide de température T₂ vaut :

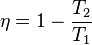
Démonstration

Cette expression ou rendement de Carnot correspond au fonctionnement cyclique et réversible d'une machine ditherme. Au cours du cycle, la source chaude à T₁ fournit la quantité de chaleur Q₁ au système moteur. Celui-ci fournit un travail W et restitue une quantité de chaleur Q₂ à la source froide à T₂.

Comme le fonctionnement est cyclique, l'état final est identique à l'état initial, donc l'énergie interne du système reste constante car c'est une fonction d'état : ΔU = 0 .

• Appliquons le premier principe: ΔU = Q₁ + Q₂ + W = 0

d'où W = - ( Q₁ + Q₂ )

• Appliquons le second principe: ΔS(syst) + ΔS(ext) = 0 si le cycle est réversible.

Q₁/T₁ + Q₂/T₂ = 0 et Q₂/Q₁ = - T₂/T₁

Le rendement du moteur correspond au rapport du travail fourni ( en valeur absolue) sur la chaleur qu'il a reçue:

η = |W| / Q₁ = |-( Q₁ + Q₂ )|/ Q₁ = 1 + Q₂/Q₁.

d'où η = 1 - T₂/T₁

Il va de soi que ce rendement correspond au cycle de Carnot réversible. C'est le rendement théorique maximal qui ne sera jamais atteint lors d'un cycle réel.

Remarques

• Cette relation montre qu'un moteur thermique monotherme ne peut fournir du travail mécanique puisque si T₁ = T₂, le rendement est nul. En fait, pour qu'il y ait du travail il faut un transfert de chaleur; celui-ci n'étant possible que si il y a une différence de température.

• Dans le cas de la machine à vapeur le rendement théorique maximal peut être calculé. Si T₁ = 373K et T₂ = 298K , on trouve η = 0,2.

Autres interprétations et conséquences du second principe

Transfert d'extensité

Une autre interprétation, plus " physique " du second principe peut être formulée. En effet, imaginons un cylindre creux fermé hermétiquement aux deux extrémités. Imaginons aussi un piston libre de se déplacer dans ce cylindre. Si l'on déplace le piston vers la gauche, la partie gauche voit sa pression augmenter et son volume diminuer et, vice-versa, la partie droite voit sa pression chuter et son volume augmenter. Si l'on relâche le piston, il va spontanément se déplacer vers la droite, vers sa position d'équilibre initiale. Le déplacement se fait donc de la partie à haute pression, qui voit son volume augmenter, vers la partie à basse pression qui voit son volume chuter. Si l'on se souvient que la grandeur intensive est ici la pression et que la grandeur extensive est ici le volume, cet exemple illustre l'énoncé suivant correspondant à une autre formulation du second principe :

L'énergie s'écoule toujours de la haute intensité vers la basse intensité par un transfert d'extensité.

Dans ce cas: δW = - p.dV

Si l'on met en contact deux objets à potentiels électrostatiques différents, l'énergie ira du plus haut potentiel (grandeur intensive) vers le plus bas par un transfert de charges (grandeur extensive): dE = v.dq .

De même, si l'on met en contact deux sources à températures différentes, la chaleur s'écoulera de la source à haute température vers celle à basse température par transfert d'entropie. L'entropie est donc l'extensité associée à la forme énergétique appelée chaleur: δQ = T.dS .

Second principe et chaos

Boltzmann a étudié le second principe sous son aspect microscopique ce qui a révolutionné la physique, mettant fin aux espoirs de Laplace fondés sur un déterminisme intégral.

Dans la statistique de Maxwell-Boltzmann, on raisonne en effet sur un grand nombre de particules indiscernables, indépendantes et identiques. Dans ce cas, l'entropie d'un macro-état Ω est défini (de façon statistique) par la formule de Boltzmann : S = k_b.ln Ω .

Ω correspond au nombre de micro-états différents observables dans un macro-état donné.

Les cycles de Poincaré

Le célèbre mathématicien Henri Poincaré démontra en 1890 un théorème extrêmement général, dont l'énoncé physique est : " Tout système macroscopique repasse une infinité de fois aussi près que l'on veut de son état initial. " Ce " théorème de récurrence " fut opposé au second principe, car il implique que toute évolution macroscopique est réversible. Pour contrer ce théorème apparemment inattaquable, Boltzmann calcula le temps nécessaire à 100 cm³ de gaz pour revenir à son état initial. Il trouva 10^E10 années !!! Autant dire que, si le problème des cycles de Poincaré subsiste, il n'est pas d'une urgence brûlante (voir dans le même ordre d'idée, l'exemple du jeu de 52 cartes, désordonné dans entropie).

La boîte de Maxwell

Soit une boîte circulaire plate, horizontale, séparée par un diamètre en 2 compartiments égaux, et contenant N palets blancs et N palets noirs, de même rayon r, glissant sans frottements sur ce fond. Ouvrir le diamètre d'une grandeur supérieure à 2r, pour permettre le passage des pions. Secouer, puis immobiliser la boîte : il est assez intuitif que l'état le plus souvent réalisé est celui pour lequel il y aura N/2 palets blancs et N/2 palets noirs dans le compartiment 1 ; ceci avec d'immenses fluctuations, d'autant plus grandes en valeur absolue que la boîte sera grande et que N sera grand : ces fluctuations croissent comme . Mais plus N est grand, plus ces fluctuations seront négligeables devant N et la répartition se rapprochera de N/2 pour chaque couleur de palet dans chaque compartiment. On remarque ici un autre aspect du second principe qui montre que l'évolution spontanée d'un système va toujours vers l'homogénéité.