Atmosphère isotherme - Définition

L'atmosphère isotherme est un modèle simpliste d'atmosphère dans lequel on considère la température comme constante et égale à T₀. Cette hypothèse conduit à une décroissance exponentielle de la pression p(z) avec l'altitude, en .

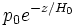
En effet, l'équation locale de la statique des fluides donne , soit avec la symétrie du problème, et dans un champ de pesanteur uniforme g, .

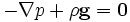
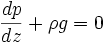
Or, la loi des gaz parfaits donne où M est la masse molaire de l'air et R la constante des gaz parfaits.

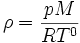
On obtient ainsi l'équation différentielle : avec , de solution .

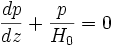
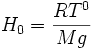
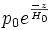
Il apparaît dont une hauteur d'échelle ou distance caractéristique du problème .

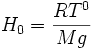
On peut remarquer que cette loi de distribution de la pression suit la loi statistique de Boltzmann : avec , où k_B est la constante de Boltzmann et m la masse d'une molécule, l'exponentielle fait apparaître le rapport de mgz, l'énergie potentielle de pesanteur d'une particule, et de k_BT, son énergie d'agitation thermique: à cause du poids , tout l'air devrait se retrouver au sol ; mais l'agitation thermique, jointe aux lois de Fick donne cette épaisseur caractéristique H₀.

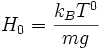
L'application numérique donne une hauteur caractéristique de 8 km. À 24 km pour une température de 0°C de l'atmosphère, il n'y aurait plus que 5% de la pression ! Cela montre les limites de ce modèle ; en réalité, le dioxygène, plus lourd, a une hauteur d'échelle différente de celle du diazote ; l'air n'est pas un gaz parfait ; et surtout, la plupart du temps dans la troposphère l'air se refroidit avec l'altitude.

En revanche, ce modèle prévoit correctement que la pression varie peu sur de faibles hauteurs dans des gaz, qui ont de faibles masses volumiques.