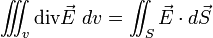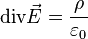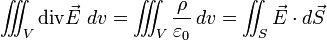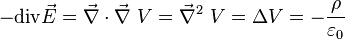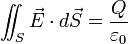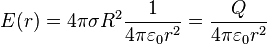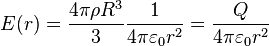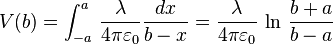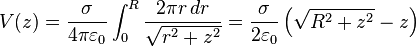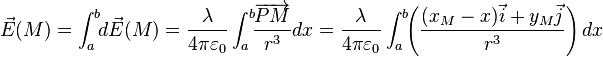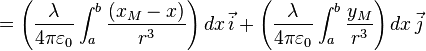Électrostatique - Définition
L'électrostatique traite des charges électriques immobiles et des forces qu'elles exercent entre elles, c’est-à-dire de leurs interactions.
Il est difficile de faire des sciences physiques sans connaître et utiliser les outils mathématiques des formules d'électrostatique.
La loi de Coulomb et le principe de superposition permettent de déduire mathématiquement les mesures expérimentales de charges immobiles. Cet état est naturellement peu courant mais constitue une étape nécessaire dans la compréhension des lois de l'électromagnétisme et de son extension : l'électrodynamique quantique relativiste.
L'électrostatique s'est révélée particulièrement performante en biophysique dans l'étude des protéines.
Généralités
Il existe une expérience simple, que tout le monde peut faire, permettant de percevoir une force électrostatique : il suffit de frotter une règle en plastique avec un chiffon bien sec et de l'approcher de petits bouts de papier. Les papiers se collent à la règle. L'expérience est simple à réaliser, cependant l'interprétation n'est pas simple puisque, si la règle est chargée par frottement, les bouts de papiers ne le sont a priori pas ! Autre expérience du même style : un filet d'eau est dévié si on approche un film de cellophane.
Plus simplement, tout le monde a reçu une décharge en attrapant un chariot par temps très sec ou en descendant ou montant dans une voiture. Ce sont des phénomènes où il s'est produit une accumulation de charges, d'électricité, d'électricité statique .
À partir de là, on peut considérer deux catégories de corps: les isolants où l'état d'électrisation se conserve localement et les conducteurs où cet état se répartit sur la surface du conducteur.
On constate aussi expérimentalement qu'il existe deux sortes de charges que l'on distingue par leurs signes, et que la matière est constituée de particules de charges variées, toutes multiples de celle de l'électron, appelée " charge élémentaire " ; cependant en électrostatique on se contentera de dire que lorsque un objet est chargé en volume, il contient une densité volumique de charge ρ(x,y,z). Ceci correspond à une approximation statistique, compte tenu de la petitesse de la charge élémentaire.
Formules de base de l'électrostatique
L'équation fondamentale de l'électrostatique est la loi de Coulomb, qui décrit la force d'interaction entre deux charges ponctuelles. Dans un milieu homogène, le seul cas que nous considérerons dans cet article, le vide par exemple, elle s'écrit :
|
|
Ici, la constante ε est une constante caractéristique du milieu, appelée la " permittivité ". Dans le cas du vide, on la note ε0. Noter que la permittivité de l'air est de 0,5 ‰ supérieure à celle du vide, et lui est donc souvent assimilée.
Notez que deux charges de même signe se repoussent et que deux charges de signes contraires s'attirent proportionnellement au produit de leurs charges et inversement proportionnellement au carré de leur distance ; notez aussi que les forces sont de valeur égale et de sens opposé (principe de l'action et de la réaction).
Comme en gravitation, l'action à distance se fait par l'intermédiaire d'un champ : le champ électrique :
Produit par 1 en 2 :
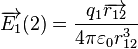
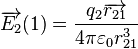
Le champ créé en M par n charges qi situées en des points Pi est additif (principe de superposition). Dans le cas d'une distribution de charges discrète :
Dans le cas d'une distribution ρ de charges continue dans l'espace, le champ causé par un petit volume chargé vaut :
et en intégrant sur tout l'espace où il y a des charges, on obtient:
où ρ est la densité volumique de charge en Pi,
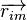
Le potentiel électrique (dont les différences s'appellent tensions) est une notion courante et importante de l'électrostatique : c'est une fonction scalaire dans l'espace, dont le champ électrique est le gradient.
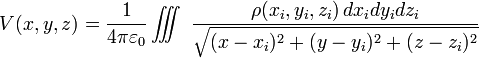
|
et en calculant les dérivées partielles
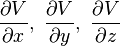
|
|
Toute l'électrostatique dans un milieu homogène est dans ces dernières formules, quoiqu'il faille remarquer que ces formules ne sont pas définies si le point de coordonnées (xi, yi, zi) porte une charge ponctuelle, ce qui n'est d'ailleurs qu'une approximation non-physique (ρ devrait y être infini).
Potentiel en 1/r et champ à divergence nulle
On place la charge qui produit le potentiel en O et on regarde en le potentiel produit en M et son gradient. Tout ce paragraphe suppose que O et M ne coïncident pas ; sinon les formules n'auraient aucun sens. Posons :
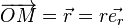
Rappelons que, par définition des dérivées partielles :
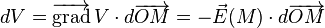
- sachant que l'on peut démontrer que
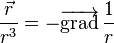
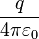
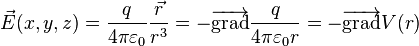
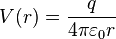
- les champs en
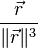
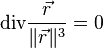
Théorème de Gauss
- Le Théorème de flux-divergence est un théorème d'analyse vectorielle, utilisable en électrostatique pour obtenir une équation locale du champ électrique.
Ce théorème indique que (démonstration sommaire) :
![[E_x(x+dx)-E_x(x)]dy\,dz+[E_y(y+dy)-E_y(y)]dz\,dx+[E_z(z+dz)-E_z(z)]dx\,dy =](https://static.techno-science.net/illustration/Definitions/autres/8/8d0eebee3d0fb8c7545d1d63ebf462e0_8395655cf564bc9fa9be9b954b897c4b.png)
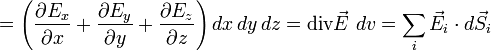
Ici dv = dx dy dz représente un volume élémentaire, que l'on peut considérer comme un parallélépipède et les dSi représentent les contributions des 6 faces, chacune étant de longueur égale à sa surface et orientée perpendiculairement à la face, vers l'extérieur. Si l'on divise un grand volume v en volumes élémentaires et si l'on somme sur tous ces volumes élémentaires, les contributions des faces situées à l'intérieur du volume se compensent exactement, et il ne reste que la contribution de la surface extérieure :
|
|
pour n'importe quel volume. En particulier, considérons une sphère chargée en volume par une densité volumique de charge ρ, ayant son centre en O et de rayon r suffisamment petit pour qu'on puisse négliger les variations de ρ :
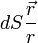
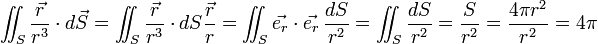
Ce qui signifie que le résultat ne dépend pas de r ! et si on multiplie par
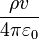
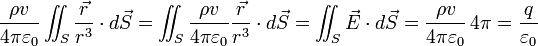
où q est la charge totale ρv de la sphère
Soit au final :
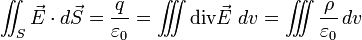
D'où (Théorème de Gauss sous sa version locale) :
|
|
et l'expression intégrée, connue par les physiciens sous le nom de théorème de Gauss :
|
|
L'équation de Poisson
| Article d'analyse vectorielle | |

|
|
| Objets d'étude | |
| Champ vectoriel | Champ scalaire |
| Équation aux dérivées partielles | |
| de Laplace – de Poisson | |
| Opérateurs | |
| Nabla | Gradient |
| Rotationnel | Divergence |
| Laplacien scalaire | Bilaplacien |
| Laplacien vectoriel | D'alembertien |
| Théorèmes | |
| de Green | de Stokes |
| de Helmholtz | de flux-divergence |
| du gradient | du rotationnel |
combine les relations précédentes pour donner une relation locale entre la distribution de charge et le potentiel :
|
|
Voir l'article Nabla pour la signification du symbole très utile

On retrouve le fait que les influences des différentes charges s'ajoutent linéairement,c'est-à-dire que pour connaître la force exercée sur une charge par plusieurs autres charges, il suffit de calculer la force qu'exercerait chacune des charges prise isolément, et d'additionner les résultats : on retrouve bien le principe de superposition, autre manière d'exprimer la linéarité de la loi de Coulomb.
La loi de Coulomb est très proche de l'expression des forces gravitationnelles ; mais ces dernières sont (pour une particule donnée) beaucoup plus faibles. Pourtant, les forces électrostatiques ont peu d'effet à grande échelle, tandis que la gravitation explique le mouvement des astres.
Cela provient du fait qu'en moyenne, la matière contient autant de charges positives que de charges négatives et donc, au-delà de l'échelle des inhomogénéités, leurs influences se compensent. Pour la gravitation, au contraire, dont l'expression de la force a un signe opposé à celui de l'électrostatique, bien que les masses aient toutes le même signe positif, elles s’attirent toutes, au lieu de se repousser comme le font des charges électriques de même signe.
Champ électrique créé par quelques distributions de charges
Les champs électriques peuvent rarement être calculés analytiquement par le calcul direct de la dernière formule mais peuvent toujours être calculés numériquement, surtout avec les progrès de l'informatique.
Lorsqu'il existe des symétries, on peut souvent faire le calcul en appliquant le théorème de Gauss au champ électrique :
-
- Le flux du champ électrique à travers une surface fermée S est proportionnel à la somme des charges qui sont à l'intérieur de cette surface.
Voici quelques exemples de résultats de calcul pour des distributions de charges symétriques.
- Fil rectiligne infini, pris suivant l'axe Oz de densité linéique de charge λ, à distance r du fil :
Pour un point M , le plan passant par M contenant l'axe Oz est un plan de symétrie, ainsi que celui passant par M et perpendiculaire à l'axe Oz ; on en déduit que le champ résultant n'a de composante que suivant :
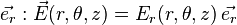
Les invariances par translation suivant Oz et par rotation suivant θ permettent de déduire que Er ne doit pas dépendre des variables z et θ et donc :
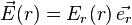
Si pour appliquer le théorème de Gauss, on choisit un cylindre passant par M, d'axe Oz, de rayon r et d'épaisseur élémentaire dz :
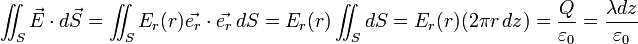
-
-
- et on obtient finalement :
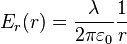
- et on obtient finalement :
-
- Plan infini, uniformément chargé en surface, de densité surfacique de charge σ, à distance r du plan. Comme le système est invariant par translation parallèle au plan, le champ ne peut être que perpendiculaire au plan. D'autre part, les champs sont directement opposés en deux points symétriques par rapport au plan. Si M est à la distance r du plan, considérons un prisme élémentaire symétrique par rapport au plan et dont une base, de surface dS, passe par M :
-
-
-
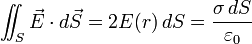
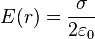
-
-
- La valeur absolue du champ est constante dans tout l'espace. Son sens change entre les deux côtés du plan ; il est donc discontinu au niveau du plan.
- Sphère creuse de diamètre R, uniformément chargée en surface, de densité surfacique de charge σ, à distance r du centre :
- à l'intérieur (r < R) :
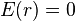
- juste à l'extérieur de la surface (r = R+0) :
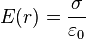
- à l'extérieur (r > R) :
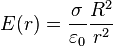
- à l'intérieur (r < R) :
- Sphère pleine de diamètre R, uniformément chargée en volume, de densité volumique de charge ρ, à distance r du centre :
- à l'intérieur (r < R) :
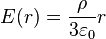
- à la surface (r = R) :
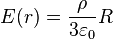
- à l'extérieur (r > R) :
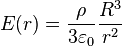
- à l'intérieur (r < R) :
- Conséquence du théorème de Gauss, nous retrouvons dans les deux cas à l'extérieur de la sphère un champ égal à celui d'une charge Q ponctuelle placée au centre de la sphère :
-
respectivement :
Exemples de potentiels
- Potentiel d'un fil fini (-a,a) en b dans son prolongement :
- Potentiel d'un disque chargé de rayon R à une distance z de son centre le long de son axe :
Un fil fini : calcul direct du champ produit
Supposons que l'on a l'axe des x chargé sur un segment AB avec une densité de charge linéique constante λ et, un point M (xM,yM) dans le plan xOy où l'on veut déterminer le champ produit par les charges réparties sur AB.
Considérons le point P(x,0) . Il est dans un intervalle dx de AB ayant une charge λdx. Ces charges créent en M un champ. Posant PM = r :
Il reste à faire les deux intégrales sur x pour obtenir les composantes de :
En constatant que :
-
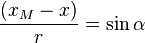
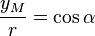
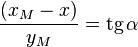
-
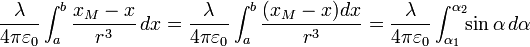
On a utilisé :
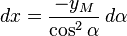
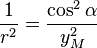
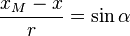
Distributions ayant des symétries et des invariances
Pour une distributions de charge ayant une symétrie par rapport à un plan, il est facile de déduire que pour un point M du plan de symétrie, le champ résultant E(M) n'a de composantes que dans le plan de symétrie (la composante perpendiculaire au plan de symétrie s'annule : en regroupant les charges par paires symétriques, on constate cette nullité).
Exemple: Si on a une distribution sphérique de charge de centre O, alors tout plan passant par O est un plan de symétrie : en conséquence, le champ résultant en M est dans tous les plans contenant OM et donc
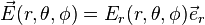
Plus généralement, si, pour une transformation euclidienne T, la distribution ρ(T(M)) est identique à ρ(M), le champ en T(M) sera le transformé par T de celui en M. On dit que la distribution est invariante par la transformation T.
C'est le cas, pour une distribution sphérique, par toute rotation autour du centre et on en déduit que le champ est purement radial, et sa valeur mesurée le long du rayon ne dépend que de sa distance au centre. En coordonnées polaires :
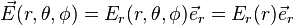
Ce résultat simplifie beaucoup les calculs.
Autre exemple : cas d'une symétrie cylindrique, avec invariance de ρ par symétrie par rapport à tout plan contenant Oz, ou perpendiculaire à Oz, on obtient :
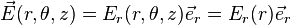
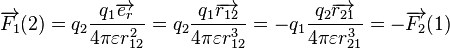
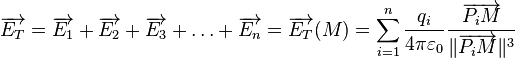
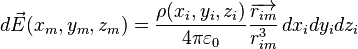
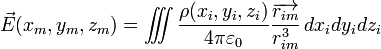
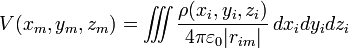
![\vec{E}(x,y,z) = \frac{1}{4 \pi \varepsilon_0}\int\!\!\!\!\int\!\!\!\!\int\!\!\rho(x_i,y_i,z_i)\,\frac{ (x-x_i)\vec{e_x}+(y-y_i)\vec{e_y}+(z-z_i)\vec{e_z}} {[(x-x_i)^2+(y-y_i)^2+(z-z_i)^2]^{3/2}}\,dx_idy_idz_i](https://static.techno-science.net/illustration/Definitions/autres/0/0a41b7021c575008a03e05677faaee6e_2559c2d17e3b635f068cc2d234b21ec1.png)