Mobilité des porteurs de charge - Définition

On se place dans un matériau possédant des porteurs libres de charge q, auquel on applique un champ électrostatique permanent (noter aussi l'absence de champ ). Appliquons alors le principe fondamental de la dynamique dans le référentiel du conducteur supposé galiléen (voir force électromagnétique) :

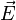
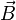
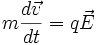
d'où

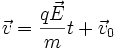
Par conséquent la vitesse diverge et donc le vecteur densité de courant aussi car " >

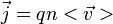
par conséquent l'intensité diverge, ce qui est impossible.

Il faut donc que la vitesse tende vers une valeur finie.

De plus est colinéaire à (en l'abscence de ), on pose donc :

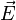
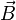
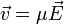
μ est dit la mobilité, il dépend du matériau, du porteur de charge, de la température, de ,...