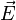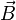Jauge de Lorenz - Définition

La jauge de Lorenz est une équation d'électromagnétisme. qui tient son nom du physicien danois Ludwig Lorenz (elle est souvent attribuée, à tort, au physicien Hendrik Lorentz probablement car celle-ci est invariante sous les transformations de Lorentz). L'introduction d'une équation de jauge permet de caractériser le potentiel vecteur A qui n'est pas défini de manière unique à partir du champ magnétique. Cette jauge particulière s'est avérée pratique et permet une description totalement relativiste de l'électrodynamique : le potentiel scalaire et le potentiel vecteur seront les composantes du quadri-vecteur potentiel.

L'équation est la suivante :

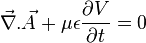
En statique elle s'écrit , on l'appelle alors jauge de Coulomb.

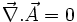
Son origine provient du fait que disposant des équations de Maxwell, on montre que la propagation des champs et dans le vide vérifie l'équation de d'Alembert (voir établissement de l'équation de propagation à partir des équations de Maxwell).

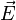
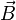
Dans cette jauge, on peut montrer que le potentiel scalaire V vérifie lui aussi l'équation de d'Alembert.

Maxwell-Gauss dans le vide s'écrit :

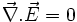
or avec Maxwell-Faraday :

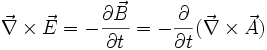
donc

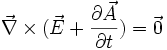
donc est un gradient et donc pour être cohérent avec l'expression en statique , il faut :

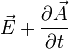
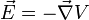
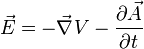
L'équation de Maxwell-Gauss devient alors :

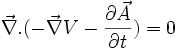
donc

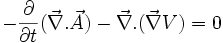
Il faut donc poser (c'est la jauge de Lorenz) pour avoir :

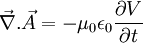
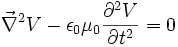
De plus, on constate que cette jauge permet aussi au champ de vérifier l'équation de d'Alembert. Il suffit d'écrire que :

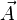
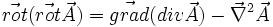
or

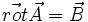
alors avec Maxwell-Ampère dans le vide (donc le vecteur densité de courant )est nul:

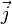
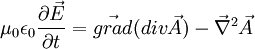
or on a toujours :

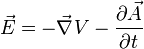
donc

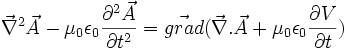
par conséquent avec la jauge de Lorenz , de vérifie l'équation de d'Alembert :

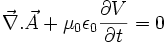
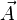
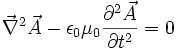
La jauge de Lorenz est donc la condition sur les potentiels (vecteur et scalaire) pour qu'ils se déplacent de la même manière que les champs et .