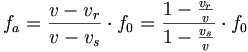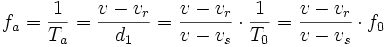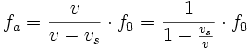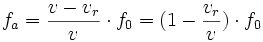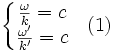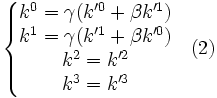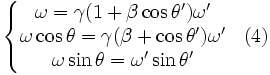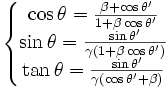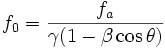Effet Doppler-Fizeau - Définition

L'effet Doppler-Fizeau est le décalage entre la fréquence de l'onde émise et de l'onde reçue lorsque l'émetteur et le récepteur sont en mouvement l'un par rapport à l'autre ; il apparaît aussi lorsque l'onde se réfléchit sur un objet en mouvement par rapport à l'émetteur ou au récepteur.

Cet effet fut proposé par Christian Doppler en 1842 dans l'article Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels, confirmé sur les sons par le chercheur néerlandais Christoph Hendrik Diederik Buys Ballot (en utilisant des musiciens jouant une note calibrée sur un train de la ligne Utrecht-Amsterdam), et également proposé par Hippolyte Fizeau sur les ondes électromagnétiques en 1848. On le désigne parfois simplement sous le nom d'effet Doppler.

Ceci explique que la hauteur du son du moteur de voiture, ou d'une sirène d'un véhicule d'urgence, est différent selon que l'on est dedans (l'émetteur est immobile par rapport au récepteur), que le véhicule se rapproche du récepteur (le son devient plus aigu) ou qu'il s'éloigne (le son devient plus grave).  ^? Reconstitution du passage d'une voiture Fiche

Cet effet est utilisé pour mesurer la vitesse avec les cinémomètres et les radars, ou bien pour des examens médicaux (notamment les échographies en obstétrique ou en cardiologie). Il explique aussi le phénomène de décalage vers le rouge (red shift) en astronomie.

Explication physique

Une personne est debout dans l'eau, au bord du rivage. Des vagues lui arrivent sur les pieds toutes les dix secondes. La personne marche, puis court en direction du large : elle va à la rencontre des vagues, celles-ci l'atteignent avec une fréquence plus élevée (par exemple toutes les huit secondes, puis toutes les cinq secondes). La personne fait alors demi-tour et marche puis court en direction de la plage ; les vagues l'atteignent avec une fréquence moins élevée, par exemple toutes les douze, puis quinze secondes.

Il est à noter que la fréquence des vagues ne dépend pas du mouvement de la personne par rapport à l'eau (elle est notamment indépendante de la présence ou non d'un courant), mais du mouvement de la personne par rapport à l'émetteur des vagues (en l'occurrence un lieu au large où le courant s'oppose au vent).

De manière symétrique, on peut imaginer une source mobile de vagues, par exemple un aéroglisseur dont le jet d'air génèrerait des vagues à une fréquence régulière. Si l'aéroglisseur se déplace dans une direction, alors les vagues sont plus resserrées vers l'avant du mouvement et plus espacées vers l'arrière du mouvement ; sur un lac fermé, les vagues frapperont la berge à des fréquences différentes.

Formulation mathématique

Effet Doppler-Fizeau galiléen

Supposons que l'émetteur et le récepteur se déplacent sur une droite munie d'un référentiel galiléen. Il y a trois référentiels à considérer :

• (1) Le référentiel du milieu dans lequel se propage l'onde (par exemple l'atmosphère pour une onde sonore). On note v la vitesse de l'onde dans ce référentiel.
• (2) Le référentiel lié à l'émetteur (source) : appelons v_s la vitesse algébrique de l'émetteur (source) par rapport au référentiel (1).
• (3) Le référentiel lié au récepteur : appelons v_r la vitesse du récepteur par rapport au référentiel (1).

Si ƒ₀ est la fréquence de l'onde dans le référentiel de la source, alors le récepteur va recevoir une onde de fréquence ƒ_a (fréquence apparente)

En effet, supposons que la source émette des bips à une fréquence ƒ₀ et que le mouvement relatif entre émetteur et récepteur se fasse selon la droite les joignant. Lorsque le deuxième bip est produit, le premier bip a parcouru une distance

d₀ = v·T₀

dans le référentiel (1), avec T₀ = 1/ƒ₀. La source s'étant déplacée de v_s·T₀ pendant le temps T₀, la distance séparant deux bips est

d₁ = (v - v_s)·T₀.

Calculons le temps T_a séparant la réception des deux bips par le récepteur. Ce dernier reçoit le premier bip. Au bout de ce temps T_a, il a parcouru la distance v_r·T_a au moment où il reçoit le deuxième bip. Ce deuxième bip aura donc parcouru la distance

d₂ = d₁ + v_r·T_a = v·T_a,

ce qui donne bien :

Si seule la source est mobile par rapport au référentiel (v_r = 0), on a alors :

et si seul le récepteur est mobile par rapport au référentiel (v_s = 0), on a :

On voit clairement que les deux situations ne sont pas symétriques : en effet, si le récepteur " fuit " l'émetteur à une vitesse supérieure à v, il ne recevra jamais d'onde, alors que si l'émetteur fuit un récepteur immobile, celui-ci recevra toujours une onde. On ne peut pas inverser le rôle de l'émetteur et du récepteur. Dans le cas classique, il y a dissymétrie dans le décalage fréquentiel selon que l'émetteur ou le récepteur est en mouvement (les fréquences reçues diffèrent par les termes du second ordre pour une même fréquence d'émission) . Cette dissymétrie est due à la présence du milieu dans lequel se propagent les ondes, elle est justifiée pour les ondes sonores. Pour les ondes électromagnétiques, la propagation pouvant se faire dans le vide, cette dissymétrie est infondée. L'effet Doppler Fizeau n'est qu'un effet de changement de référentiel, il faut considérer dans ce cas l'émetteur et le récepteur à la vitesse -v/2 et v/2, ce qui donne le même décalage fréquentiel avec l'émetteur ou le récepteur en mouvement, la vitesse radiale relative donne le changement de fréquence. La symétrie est rétablie dans la relativité Galiléenne.

En conclusion, s'il faut distinguer la propagation des ondes sonores de celle des ondes électromagnétiques, c'est par la présence du milieu ou du vide dans lequel se fait la propagation.

Si l'émetteur et le récepteur sont immobiles dans le référentiel mais que l'onde se réfléchit sur un objet en mouvement, alors tout se passe comme si c'est le récepteur qui était à la place de l'objet en mouvement.

Notons aussi que dans le cas d'ondes électromagnétiques, la vitesse de l'onde est c qui dépend de la nature du milieu (et notamment de son indice de réfraction), mais pas du référentiel.

Effet Doppler-Fizeau relativiste

En relativité, il n'y a plus que deux référentiels, celui de deux observateurs dans des référentiels différents, qui observent la propagation d'une onde électro-magnétique. Le premier observe une onde de pulsation ω, le second observe la même onde avec une pulsation ω', la vitesse relative des deux observateurs est v. Il s'agit de relier ω' à ω et v. Afin de comparer la relativité restreinte avec la relativité galiléenne, nous pourrons supposer que l'onde est émise par le premier observateur et reçue par le second.

Nous allons développer dans ce qui suit comment les angles associés aux trajectoires des rayons lumineux se transforment en relativité restreinte, et ensuite nous verrons l'effet Doppler-Fizeau relativiste.

Soit un rayon lumineux émis dans le référentiel R caractérisé par une pulsation ω et un vecteur d'onde . Ce rayon se propage dans la direction donnée par le vecteur d'onde et .

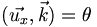
Dans le référentiel R', en translation rectiligne uniforme par rapport au premier référentiel dans la direction des x, à la vitesse v, le même rayon est caractérisée par une pulsation ω' et un vecteur d'onde . Ce rayon se propage dans la direction donnée par le vecteur d'onde et .

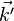
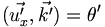
On sait que :

De plus les transformations de Lorentz entre un quadrivecteur (k⁰,k¹,k²,k³) du référentiel R et un quadrivecteur (k'⁰,k'¹,k'²,k'³) du référentiel R' sont :

avec et .

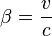
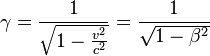
En prenant une onde se propageant dans le plan Oxy (ou O'x'y'), les deux quadrivecteurs sont ici  :

et

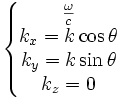
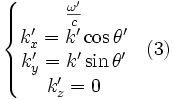
Les transformations de Lorentz donnent compte tenu de (1) (2) (3) :

Nous obtenons les relations transformant les angles :

La relation inversée donnant la transformation du cos donne : . Ces relations interviennent d'ailleurs dans le phénomène d'aberration de la lumière (l'angle de propagation de la lumière n'est pas le même dans les deux référentiels).

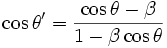
On obtient en insérant dans (4) et en divisant par 2π pour obtenir des fréquences :

où f₀ est la fréquence dans le référentiel R et f_a la fréquence dans le référentiel R'.

• Si R' est à droite de R, l'observateur s'éloigne de la source et on a θ = 0, décalage vers le rouge (f_a < f₀) :

ou bien .

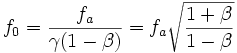
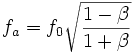
Cette expression de f_a est légèrement différente de l'expression donnée par l'effet Doppler-Fizeau galiléen, qui était , mais identique au second ordre en β. On voit que les deux référentiels jouent des rôles symétriques, en relativité galiléenne pour les ondes électromagnétiques, par opposition au cas des ondes sonores par exemple.

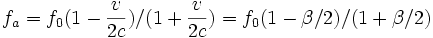
• Si R' est à gauche de R, l'observateur se rapproche de la source, et on a décalage vers le bleu (f_a > f₀) :

ou bien

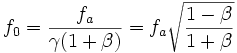
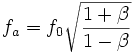
Applications

En médecine

En 1958, le doppler continu (qui est un cristal émettant et recevant en continu des ultrasons) permit l'étude de la circulation sanguine dans les vaisseaux (Rushmer). Le premier doppler pulsé (émission de l'ultrason en discontinu et fenêtre d'écoute temporelle fixée, permettant d'analyser la vitesse du sang à une profondeur définie) a été introduit par Baker en 1970.

• Le doppler, couplé ou non à un examen échographique, permet d'analyser la vitesse du sang. On peut ainsi quantifier des débits, des fuites ou des rétrécissements.
• En cardiologie, on peut analyser la vitesse des parois cardiaques à l'aide du doppler tissulaire, c'est l'imagerie doppler des tissus, ou TDI (tissular dopplar imaging)

En métrologie

L'effet doppler est utilisé par le vibromètre laser pour la mesure de vibrations en mécanique. Il est utilisé aussi par les anémomètres laser (LDV) pour la mesure de vitesses d'écoulement des fluides.

Circulation routière

L'effet doppler permet à la police et à la gendarmerie de déterminer la vitesse des automobiles. Pour cela ils utilisent un radar dont la fréquence est parfaitement connue. La mesure de la fréquence de l'écho donne la vitesse du contrevenant. La technologie moderne permet aujourd'hui d'avoir des radars automatiques et des jumelles radar.