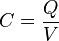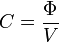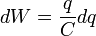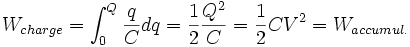Capacité électrique - Définition
Définition
La capacité représente la quantité de charge électrique stockée pour un potentiel électrique donné. Elle est définie comme étant la somme des charges électriques d'un élément divisé par le potentiel de cet élément :
ou, selon le théorème de Gauss, la capacité peut être exprimée comme étant un flux électrique par volt
où
- C est la capacité en farad
- Q est la charge en coulomb
- V est le potentiel en volt
- Φ est le flux électrique associé à la charge Q en coulomb
Energie
L'Énergie mesurée en joules) accumulée dans une capacité est égal au travail fourni pour la charger. On considère une capacité C, portant une charge +q sur une plaque et -q sur l'autre plaque. Pour déplacer une charge infinitésimale dq d'une plaque à l'autre à l'encontre d'une différence de potentiel V = q/C, il faut fournir un travail dW:
où
- W est le travail mesuré en joules
- q est la charge mesurée en coulombs
- C est la capacité mesurée en farads
On peut calculer l'énergie accumulée dans la capacité en intégrant cette équation. Si l'on part avec une capacité non chargée(q=0) et que l'on déplace les charges d'une plaque à l'autre jusqu'à avoir les charges +Q and -Q sur l'une et l'autre plaque, il faut fournir le travail W:
Si l'on combine cette relation avec celle qui donne la valeur de la capacité d'un condensateur formé de deux plaques parallèles, on obtient :
-
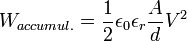
avec ε0 = 8,854.10-12 F·m-1 (permittivité électrique du vide)