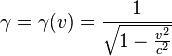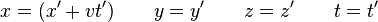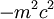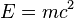Relativité restreinte - Définition

|
| Cet article de physique fait partie de la série relativité |
| Bases |
| histoire - théorie |
| Lorentz - Einstein - Mach |
| transformation de Lorentz |
| Feynman - Poincaré - Michelson |
| espace-temps-c - E=mc² - t |
| EQR |
| exp:Michelson et Morley |
| exp:pensée?-éther |
| jumeaux-train |
| relativité restreinte-générale |
| théorie de la relativité |
| controverse historique |
| Techniques |
| cyclotron |
| accélérateur de particules |
| Méta |
| article |
| Liens physique |
| Formulaire |
On nomme relativité restreinte une première version de la théorie de la relativité, émise en 1905 par Albert Einstein, qui ne considérait pas la question des accélérations d'un référentiel, ni les interactions d'origine gravitationnelles. Cependant, elle présentait une explication cohérente des interactions électro-magnétiques et de leurs transformations par changement de référentiel à l'aide de la transformation de Lorentz. De plus, elle résolvait des paradoxes existant en mécanique classique relatifs aux mesures de la vitesse de la lumière. Cette théorie a introduit pour la première fois la notion d'espace-temps et expliqué quelques phénomènes étonnants, mais vérifiés expérimentalement, de variation des mesures de longueur et de durée entre un observateur et un autre, chacun d'eux étant situé dans un référentiel différent.
Elle est enseignée dans le cadre de la cinématique en mathématiques et comme introduction à la relativité générale en physique pour sa clarté et sa simplicité. D'autre part, c'est actuellement la seule théorie utilisable pour représenter les effets relativistes en mécanique quantique.
La théorie a été popularisée en science-fiction, notamment en raison du phénomène de dilatation des temps, avec le célèbre paradoxe des jumeaux. Elle a eu également un impact en philosophie en éliminant toute possibilité d'existence d'un temps et de durées absolues dans l'ensemble de l'univers, implicitement admis avant elle.
La théorie
Les postulats d'Einstein (1905)
- P1 : Les lois de la physique sont les mêmes dans tous les référentiels inertiels. Rappelons que depuis Newton, un référentiel est dit inertiel si tout corps isolé y possède un mouvement rectiligne uniforme, c’est-à-dire un vecteur vitesse

- P2 : La vitesse de la lumière dans le vide a la même valeur dans tous les référentiels inertiels [1].
Commentaires
- Le premier postulat est le principe de relativité proprement dit, dans sa conception restreinte à la classe des référentiels inertiels. Il formalise une intuition de Galilée selon laquelle le mouvement rectiligne uniforme est " comme rien " pour l'observateur appartenant au référentiel mobile.
- Le second postulat permet en pratique une synchronisation des horloges fixes d'un référentiel donné, en tout endroit de ce référentiel : l'utilisation des signaux lumineux permet au gardien du temps (par exemple, placé au centre du référentiel) de faire mettre à l'heure toutes les horloges fixes de son référentiel.
On notera que ces postulats ont été énoncés alors que seuls deux types d'interaction avaient été totalement cernés par les physiciens : la gravitation (loi de Newton de 1687) et l'électromagnétisme de Maxwell -Lorentz (1865-1895). Les postulats s'appliqueront aussi aux interactions à découvrir.
Utilité du second postulat ?
Il est très remarquable que l'on puisse entièrement se passer du second postulat P2 pour déterminer les équations des transformations de Lorentz, à condition d'introduire une hypothèse supplémentaire au postulat P1 : l'espace-temps est homogène et isotrope . Ce fait, qui demeure toujours aussi mal connu aujourd'hui, a été découvert dès 1910 par Kunz[2] et Comstock[3] indépendamment. On obtient alors un groupe de transformations à un paramètre c, physiquement homogène à une vitesse. Ces transformations s'identifient :
- aux transformations de Galilée si c2 est infini.
- aux transformations de Lorentz si c2 est fini positif [4].
Le lecteur intéressé par cet aspect peut consulter par exemple [LL77], ou encore le paragraphe 2.17 : Special relativity without the second postulate de [RI77].
Les transformations de Lorentz et les calculs relativistes qui s'en déduisent
Dans le cadre des transformations spéciales, les hypothèses d'Einstein mènent aux transformations suivantes :
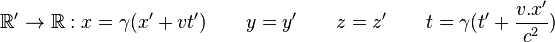
où γ est un facteur scalaire sans dimension défini par
Les transformations de Lorentz sont les transformations de référentiels pour lesquelles les équations de Maxwell restent invariantes. La loi de Newton-Lorentz (loi de Newton relativiste) reste aussi invariante sous ces transformations (l'équation de Newton a été modifiée justement pour satisfaire l'invariance sous ces transformations).
A la limite des faibles vitesses (du référentiel

Pour de plus amples informations concernant l'établissement des relations de transformations, voir ci-dessous ou l'article détaillé Transformations de Lorentz.
Les transformations de Lorentz mènent à une vision totalement neuve de la physique ; en particulier le temps n'est plus absolu, pas plus qu'il n'existe de temps de référence plus privilégié que les autres. D'une façon générale, en ce qui concerne la cinématique, les conséquences sont nombreuses. Précisons-en quelques unes.
Conséquences
- la dilatation des durées : un phénomène physique durant un intervalle de temps dans un référentiel, dure une quantité différente dans un autre référentiel.
- Supposons un intervalle de temps Δt0 correspondant à l'intervalle entre deux battements de cœur d'un individu, entre deux tocs d'une horloge, immobiles dans le référentiel

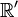

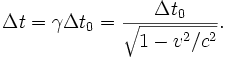
- Ainsi, le même phénomène durant 1 s (par exemple) dans un référentiel où il est au repos est vu durer γ s dans le référentiel par rapport auquel le sujet du phénomène se déplace à la vitesse v : une horloge mobile apparaît ralentir.
- Il faut insister ici sur la signification de la notion de durée entre deux événements dans un référentiel. La méthode de mesure consiste à attribuer comme coordonnée temporelle d'un événement l'instant lu sur l'horloge fixe du référentiel à l'endroit où se passe cet événement. Ainsi la durée la plus courte est-elle celle qui correspond au référentiel associé au phénomène (au voyageur, à son horloge propre) ; elle n'est lue que par l'intermédiaire d'une seule horloge, on lui attribue le nom de durée de temps propre.
- Pour tout référentiel par rapport auquel le voyageur se déplace la durée du phénomène demande, pour sa mesure, deux horloges, une à chacun des points du référentiel où se trouvera le voyageur à l'instant initial et à l'instant final. C'est cette durée à laquelle il faut comparer la durée propre.
- Les vérifications expérimentales sont nombreuses : durée de vie de muons atmosphériques, durée de vie de particules dans les accélérateurs... marches des horloges embarquées des satellites (le phénomène sert dans ce cas à séparer des effets de la gravitation).
- la contraction des longueurs dans la direction du déplacement : supposons que dans le référentiel
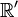
- Dans le référentiel



- Cette méthode appliquée à partir des relations de transformation fournit :
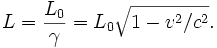
- La longueur de la règle mobile est donc plus courte (que sa longueur propre) dans tout référentiel par rapport auquel elle se meut.
- Les vérifications expérimentales sont un peu différentes que celles citées plus haut : dans le référentiel des muons traversant l'atmosphère à grande vitesse, c'est l'atmosphère qui se meut, mais de plus l'épaisseur d'air traversée n'est plus quelques kilomètres, mais quelques centaines de mètres...
- Cette contraction avait été envisagée par Fitzgerald, et soutenue ensuite par Poincaré.
- la relativité de la simultanéité : la modification des valeurs des durées entre deux événements lors du passage d'un référentiel à l'autre devient spectaculaire dans le cas d'événements simultanés. La relativité, via la possibilité de synchronisation des horloges fixes dans un référentiel donné, limite la notion de simultanéité à l'intérieur d'un référentiel galiléen. C'est d'ailleurs ce qui a permis de définir la méthode de mesure de distance ci-dessus.
- Deux événements simultanés dans



Attention : Il n'en résulte pas pour autant que deux événements quelconques pourront toujours être associés à un repère d'où on les verrait simultanés. Ce n'est vrai que sous condition d'une inégalité faisant intervenir la distance en espace-temps des deux événements.
Exemples
Illustration simple
La différence entre les durées éprouvées par deux observateurs en mouvement relatif uniforme constitue la première source d'étonnement lorsqu'on découvre la relativité restreinte. Un ouvrage de vulgarisation (voir référence) remarquable donne une idée simple sur ce problème. L'auteur considère une montre à photon dans laquelle un grain de lumière effectuerait, à la vitesse c de la lumière, des allers-retours entre deux miroirs.
Si cette montre reste fixe par rapport à l'observateur, la durée d'un aller-retour t0 est égale au quotient du trajet effectué par la célérité de la lumière. Au contraire, si la montre se déplace perpendiculairement au trajet du photon, celui-ci suit le mouvement de la montre et le segment est remplacé par une ligne brisée plus longue que lui. La célérité de la lumière restant la même, la durée t du parcours est supérieure à t0 : la montre en mouvement retarde.
Un calcul géométrique montre que, v étant la vitesse de translation de la montre, les deux temps sont reliés par
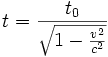
La célérité de la lumière étant de 300000 km/s, considérons un avion qui vole à 300 m/s. Sa vitesse est donc le millionième de celle de la lumière et l'erreur commise en utilisant l'approximation galiléenne est inférieure à un millionième de millionième, ce qui est tout à fait négligeable. Pour toutes les vitesses dont nous avons une expérience sensible, l'approximation galiléenne est donc très correcte.
Pour un corps se déplaçant à une vitesse égale au dixième de celle de la lumière, l'erreur commise est inférieure à un pour cent. Les effets relativistes ne deviennent donc significatifs que pour des vitesses proches de la célérité de la lumière ; c'est la raison pour laquelle nous avons de grandes difficultés à appréhender le fonctionnement de la relativité restreinte.
Enfin, cette célérité de la lumière apparaît comme une limite impossible à atteindre; on peut cependant s'en approcher autant qu'on le veut, du moins de façon purement théorique.
Paradoxe du train
Cet exemple illustre quelques-uns des effets de la relativité restreinte : non-pertinence des notions de simultanéité et d'antériorité absolues, contraction des durées et des distances.
On considère un train et un tunnel de chemin de fer qui ont (dans le même référentiel) la même longueur.
Ce tunnel est équipé de deux détecteurs, un à l'entrée, appelons-le E et l'autre à la sortie, on l'appelle S, et le train s'apprête justement à le traverser. Il est très rapide et se déplace à une vitesse proche de celle de la lumière. Le détecteur S émet un signal lumineux lorsque l' avant du train sort du tunnel. Le détecteur E quant à lui émet un signal lumineux lorsque l' arrière du train entre dans le tunnel.
Un observateur placé en bordure de voie et précisément à égale distance des deux détecteurs voit le train traverser le tunnel et constate que
- E a émis un signal avant S. Il en déduit donc que le train est plus court que le tunnel ;
- le train mettra 2 secondes pour arriver à sa destination en continuant à cette allure.
Pourtant, après être arrivé à destination, il rencontre un passager du train qui lui affirme que :
- Au contraire, c'est S qui a émis un signal avant E et que c'est bien naturel car le train était plus long que le tunnel d'après lui ;
- le train, gardant sa vitesse pratiquement jusqu'à la gare, est arrivé à destination en 1 seconde.
Qui s'est trompé ? Personne. La relativité restreinte affirme que la distance, la durée et la simultanéité sont relatives, à savoir qu'elles varient d'un référentiel à l'autre.
Ainsi le train paraît-il plus court pour un observateur placé dans le référentiel du tunnel, alors que c'est le tunnel qui paraît plus court pour un observateur assis dans le train, et tout cela par le simple fait que les deux observateurs ont des notions très différentes de la simultanéité des deux événements E et S.
Ce paradoxe est confirmé par l'expérience. Par exemple, pour un observateur immobile, une particule instable (comme un élément radioactif) met en moyenne plus de temps à se désintégrer dans un accélérateur de particule que lorsqu'elle est au repos.
Voir article relié : paradoxe des jumeaux.
Questions fréquemment posées
L'écoulement du temps est-il homogène dans tout l'univers ?
La relativité restreinte montre que la notion de référentiel absolu n'a pas de sens physique, et particulièrement en ce qui concerne l'écoulement du temps. À ce titre, on peut se demander si - dans la pratique - l'écoulement du temps est globalement le même dans tout l'univers (et par exemple si la notion "d'âge de l'univers" a un sens absolu), ou si les mouvements relatifs des différentes parties de l'univers font qu'on ne peut pas parler de référentiel absolu de temps pour tout l'univers.
En fait, cette question est tranchée par l'examen du fond diffus cosmologique, qui s'avère isotrope à 10-4 près. La température du fond cosmologique évoluant avec le temps, ce résultat ne pourrait être obtenu si différentes parties de l'univers évoluaient à des rythmes temporels notablement différents.
Ainsi, il apparaît que les différentes parties de l'univers ne sont pas en mouvement relatif les uns par rapport aux autres et que le temps évolue, à 10-4 près, de la même manière dans tout l'univers (observable), et qu'il existe donc une certaine notion de référentiel de temps global et de simultanéité absolue dans tout l'univers.
Ce résultat peut surprendre étant donné que l'expansion de l'univers provoque l'éloignement relatif des galaxies. Cependant, cet éloignement est non pas un éloignement dans l'espace mais une distension de l'espace lui-même. Ainsi, il n'est pas exclu que, du fait de l'expansion de l'univers, des galaxies s'éloignent (en apparence) plus vite que la vitesse de la lumière. Cela n'entre pas en contradiction avec la relativité restreinte, car il ne s'agit pas d'une vitesse dans l'espace, mais une apparence de vitesse due à l'extension de l'espace (de la même manière que l'inflation cosmique a éloigné, à une vitesse très supérieure à la lumière, des parties de l'espace auparavant très proches l'une de l'autre, de manière à ce qu'elles soient maintenant séparées par un intervalle de genre espace).
Bien entendu, cette constatation ne remet pas en cause le fait que l'écoulement du temps est bel et bien relatif à un référentiel donné. Simplement, il s'avère que l'univers pris dans son ensemble semble appartenir (sauf exceptions d'objets individuels dans cet univers) à peu près à un même référentiel.
Origines de la théorie
Bref historique
À la fin du XIXe siècle, James Clerk Maxwell établit les équations de l'électromagnétisme qui faisaient apparaître l'existence d'ondes électromagnétiques. Il s'avéra que les ondes lumineuses étaient de bonnes candidates à ce statut, ce qui posa un problème sérieux car leur célérité ne devait dépendre que des propriétés électriques et magnétiques du milieu.
Pour saisir la difficulté, considérons d'abord deux observateurs, le second se déplaçant en voiture à 100 km/h par rapport au premier tandis qu'un TGV roule dans la même direction à 300 km/h. Conformément à la relativité galiléenne, le train se déplace à 200 km/h par rapport au second observateur. Plus généralement, tant qu'on ne considère que des mouvements uniformes, il n'y a pas dans l'Univers d'observateur privilégié, tout observateur pouvant être choisi arbitrairement comme référence pour la description des lois de la nature. En d'autres termes, ce principe de relativité affirme qu'il n'existe pas de mouvement absolu mais seulement des mouvements relatifs.
Les équations de Maxwell disent au contraire que, si on remplace le TGV par une onde lumineuse et si le second observateur se trouve, par exemple, dans un vaisseau spatial se déplaçant à 100000 km/s par rapport au premier, les observateurs voient, tous les deux, l'onde se propager à 300 000 km/s.
Cette affirmation qui heurte le sens commun pouvait conduire à mettre en doute l'exactitude des équations de Maxwell. Albert A. Michelson et Edward W. Morley ont effectué une expérience pour comparer les valeurs de cette célérité selon un méridien terrestre et selon un parallèle. Celle-ci n'a pu mettre en évidence aucune différence significative entre les deux mesures, ce qui validait les équations.
Des formules de transformation pour passer d'un observateur à un autre furent établies par Hendrik Antoon Lorentz ; il s'agissait d'équations de compatibilité dont la signification n'était pas claire. Une explication a été alors imaginée pour justifier ces formules étranges : l'éther, milieu jugé précédemment nécessaire à la propagation des ondes lumineuses comme l'air est nécessaire à la propagation des ondes sonores, possèderait les propriétés élastiques qui conduiraient à ces équations. Henri Poincaré a alors proposé la théorie avant Einstein, après en avoir jeté les bases dans des publications antérieures. On pourra en trouver la traduction en français commentée par Anatoly A. Logunov., directeur de l'Institut de physique des hautes énergies (Protvino, Russie), membre de l'Académie des sciences de Moscou. Cet article est intitulé : Sur les articles de Henri Poincaré " Sur la dynamique de l'électron " Le texte fondateur de la relativité, en langage scientifique moderne[5].
En 1905, dans son article intitulé De l'électrodynamique des corps en mouvement[6], Albert Einstein présenta la relativité comme suit :
- L'éther est une notion arbitraire qui n'est pas utile à l'expression de la théorie de la relativité.
- La célérité de la lumière par rapport aux observateurs ne dépend pas de leur vitesse.
- Les lois de la physique respectent le principe de relativité du mouvement. Les équations de Lorentz qui en découlent représentent donc la réalité physique : un observateur attribue à un corps en mouvement par rapport à lui une longueur plus courte que la longueur attribuée à ce même corps par des observateurs ayant le même mouvement que ce corps et la durée des phénomènes qui affectent ce corps en mouvement est allongée par rapport à cette même durée mesurée par des observateurs ayant le même mouvement que ce corps.
Einstein a également réécrit les formules qui définissent la quantité de mouvement et l'énergie cinétique de manière à les rendre invariantes dans une transformation de Lorentz.
Les trois coordonnées d'espace et le temps jouant des rôles semblables dans les équations de Lorentz, le mathématicien Hermann Minkowski interpréta ces dernières dans un espace-temps à quatre dimensions. Cette présentation mathématique permit à Einstein d'améliorer la description physique du phénomène en considérant que tout corps se déplace dans l'espace-temps à la vitesse de la lumière, cette vitesse étant répartie sur les quatre axes de coordonnées.
La répartition exacte des rôles fait toutefois l'objet d'une controverse, particulièrement au cours des années 2000. (voir Controverse sur la paternité de la relativité).
Attitude du comité Nobel
" Malgré la prudence de Lorentz, la théorie de la relativité restreinte fut rapidement acceptée. En 1912, Lorentz et Einstein furent proposés pour un prix Nobel conjoint pour leur travail sur la relativité restreinte. La recommandation était de Wien, lauréat de 1911, et déclare que " bien que Lorentz doive être considéré comme le premier à avoir trouvé le contenu mathématique du principe de relativité, Einstein réussit à le réduire en un principe simple. On devrait dès lors considérer le mérite des deux chercheurs comme comparable ". Einstein ne reçut jamais le Nobel pour la relativité, le prix Nobel n'étant, en principe, jamais accordé pour une théorie pure. Le comité fut d'abord prudent et attendit une confirmation expérimentale. Le temps que cette confirmation soit enfin disponible, Einstein était passé à d'autres travaux importants. " [7]
Einstein se verra finalement décerner le prix Nobel de physique en 1921, " pour ses apports à la physique théorique, et tout spécialement pour son explication de l'effet photoélectrique "[8].
On justifie souvent l'absence de prix Nobel pour la théorie à la difficulté à discerner les mérites exacts d'Einstein et Lorentz par rapport aux autres contributeurs.
Transformations de Lorentz
Les transformations dites de Lorentz ont été déterminées avant Lorentz. Lorentz lui-même en 1906, les attribue à Voigt et indique même dans le texte: Über das Döppler'sche Prinzip, " publié en 1887 et qui à mon grand regret a échappé à mon attention pendant toutes ces années ", précise Lorentz.
Interprétation du temps par Poincaré
Qui a donné à l'ensemble le nom d'" équations de Lorentz " ? Poincaré, qui en avait entendu parler par Lorentz, et indique dans son cours de 1898 que le " temps local " que Lorentz présente comme un " paramètre fictif " n'a pas de raison de ne pas être considéré comme le temps tout court, qui serait relatif et non pas absolu. En juin 1905, ce même Poincaré signale également que l'ensemble des transformations en question forme une structure de groupe sur l'espace-temps, et que le terme x²+y²+z²-c²t² constitue un invariant du groupe. Dans un texte publié en 1915, Lorentz reconnait cette erreur de sa part.
Nous trouvons toutefois dans le livre de référence de T. Damour (physicien relativiste de niveau mondial), voir bibliographie ci-dessous, pages 33 et 34, une analyse comparée du concept de temps chez Poincaré et Einstein qui montre toute la valeur de ce qu'apporte Einstein. Citons-en quelques phrases: "Une conséquence cruciale de la limitation de l'horizon conceptuel de Poincaré est que le "temps local", dont il parle dans le texte de 1904 cité ci-dessus diffère de façon essentielle du "temps" qu'Einstein attribue à un référentiel en mouvement. En effet, une lecture attentive du texte de Poincaré de 1904, des cours qu'il donna à la Faculté des Sciences de Paris pendant l'hiver 1906-1907, et d'un article publié en 1908, montre que le "temps" dont parle Poincaré est toujours un temps dont la "seconde" est battue par des horloges en "repos absolu"" A cet égard, si l'on peut discuter le fait qu'Einstein ait lu ou non Poincaré avant juin 1905 (quand bien même il l'aurait lu, les apports d'Einstein sont incontestablement différents), il convient plutôt de se demander si Poincaré avait bien lu l'article de 1905 d'Einstein par la suite! Citons encore la conclusion de T. Damour sur le sujet: "Comme Lorentz et Poincaré pensaient toujours le temps en termes de temps universel absolu de Newton, ils n'ont jamais suggéré, comme Einstein le fit, qu'une horloge en mouvement puisse battre un temps différent de celui d'une horloge au repos"
Rotation dans un espace-temps à quatre dimensions
Poincaré mentionne en particulier : " nous voyons que la transformation de Lorentz n'est qu'une rotation autour de cet espace [à 4 dimensions] autour de l'origine regardée comme fixe ". (Sur la dynamique de l'électron, Comptes-rendus de l'Académie des Sciences, 5 juillet 1905. Le même espace, mentionné trois ans plus tard par Minkowski, prendra le nom... d'" espace/temps de Minkowski "
L'expérience d'interférométrie de Michelson et Morley
C'est en essayant d'utiliser la loi d'addition des vitesses (Michelson 1881, puis Michelson et Morley 1887) pour mettre en évidence le mouvement de la Terre par rapport à l'espace supposé immobile que ces chercheurs ont obtenu un résultat apparemment absurde : la vitesse de la Terre autour du soleil était nulle ! Certains ont essayé d'expliquer ce résultat en parlant d'éther entraîné par la Terre à la façon d'un bateau qui entraîne l'air contenu dans ses cabines, mais c'est Minkowski qui montra que les transformations de Lorentz formaient un groupe et émit l'idée d'un espace-temps non euclidien à quatre dimensions. Einstein développa alors l'idée qu'il ne s'agissait pas là d'un simple jeu intellectuel, mais bien de la réalité sous-jacente qui échappait à nos sens aux échelles de vitesse où nous travaillons communément.
Les vitesses ne s'additionnent pas arithmétiquement, et pour obtenir les règles de composition des vitesses, il suffit d'admettre les transformations de Lorentz comme valides pour toutes les lois de la nature; celles de Galilée en sont une approximation valable aux faibles vitesses.
Développements et annexes
Cette partie introduit à quelques développements de points présentés dans des pages liées ; on y trouve plusieurs approches des transformations de Lorentz.
On remarque en effet qu'il est souvent nécessaire de faire appel aux aspects mathématiques qui dans le cas présent sont un garde-fou précieux contre les raisonnements trop rapides, liés à des inconscients classiques.
Les aspects révolutionnaires de la relativité ont marqué la génération des physiciens du premier tiers du XXe siècle et ont mené à un certains nombres d'" expériences de pensée " (GedankenExperiment en allemand) permettant d'appréhender les phénomènes contre-intuitifs.
Parmi ces expériences de pensée, le paradoxe des jumeaux, énoncé en 1911 par Paul Langevin, a focalisé et focalise encore les pensées de ceux qui réfléchissent sur la relativité restreinte. On se trouve en fait devant deux aspects paraissant antinomiques (paradoxaux tous deux pour un physicien classique). D'un côté, hors des phases d'accélération (départ, retournement et freinage de celui qui s'en va), chacun des jumeaux est en mouvement relatif uniforme par rapport à l'autre : son horloge, vue du référentiel de l'autre est ralentie. D'un autre côté, lors de la rencontre finale, le voyageur, parti et revenu, est plus jeune que le sédentaire. Il existe bien sûr une asymétrie réelle entre les expériences vécues par chacun des deux jumeaux. Le jumeau voyageur subit une phase d'accélération, contrairement à son jumeau sédentaire : à ce titre, la découverte de la relativité générale, en 1915, amène une explication du vieillissement différent des jumeaux. Il faut cependant avoir conscience que ce n'est pas la phase d'accélération qui joue un rôle essentiel dans le ralentissement de l'horloge du jumeau voyageur, mais bien la dilatation des temps durant l'aller et le retour qu'il effectue dans deux référentiels inertiels différents.
Changement de référentiel
Introduction aux changements de référentiels
Une étape importante de la mise en forme de la théorie concerne les notions à introduire pour décrire le passage d'un référentiel dans un autre.
À partir du moment où l'on travaille dans l'espace-temps à quatre coordonnées, dont l'une est temporelle, mais exprimée en unités de distance, on ne s'impose a priori de conditions sur aucune des coordonnées, à part celles qui peuvent apparaître acceptables après mûre réflexion.
Ces conditions sont très simples et très efficaces. Il s'agit des hypothèses suivantes, concernant chacun des référentiels galiléens :
- l'espace-temps est homogène :
- il n'existe pas de point privilégié dans l'espace et il n'existe pas d'instant privilégié. Ainsi dans un référentiel donné l'origine du repère et le zéro de l'horloge sont sans importance.
- toute modification, par un observateur (galiléen), de l'origine du repère ou du zéro de l'horloge est vue nécessairement comme modification de l'origine du repère ou du zéro de l'horloge par n'importe quel autre observateur (galiléen)[9]. Cette condition (caractère absolu des translations d'espace-temps) implique la linéarité des changements de référentiels[10].
- l'espace-temps est isotrope : il n'existe pas de direction privilégiée dans l'espace.
Puis une condition sur une hypothèse logique minimale :
- deux événements, reliés par un lien de cause à effet dans un référentiel, doivent être reliés par un lien semblable dans un autre référentiel ; ainsi le changement de référentiel doit interdire que dans un référentiel l'effet ne précède la cause.
- deux événements coïncidant dans un référentiel, donc non reliés par un lien de cause à effet, ne coïncident pas nécessairement dans un autre référentiel galiléen (il s'agit d'une conséquence de l'impératif précédent).
Le fait est que cette hypothèse minimale permet la possibilité suivante : les horloges, fixes dans les différents référentiels peuvent paraître avoir des marches différentes, tant que cela ne modifie pas l'ordre temporel imposé par la causalité.
Ces conditions sont mises en œuvre dans la recherche des transformations de Galilée, puis de celles de Lorentz qui sont abordées ci-dessous. L'on travaille, en général, dans le cadre de transformation dites spéciales caractérisées par le fait que les systèmes d'axes x,y,z et x',y',z' sont choisis tels qu'ils soient parallèles, que les axes O’x’ et Ox soient communs et parallèles à la vitesse

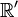

Une seconde étape nécessaire au développement des calculs est la mise à zéro des horloges fixes dans chacun des référentiels. Usuellement on choisit de régler sur 0, les horloges fixes, respectivement en O’ et O, lorsque les deux points coïncident. Les horloges fixes de chacun des référentiels sont ensuite synchronisées sur celles de O’ et O, respectivement.
Les transformations de Galilée imposent l'hypothèse de Newton sur le temps, identique dans tous les référentiels, elles vérifient donc sans difficulté l'hypothèse sur la conservation de la causalité.
Les transformations de Galilée
Les transformations de Galilée correspondent donc à un choix d'un temps unique, universel, indépendant des référentiels, ...absolu. Compte tenu des conditions d'homogénéité et d'isotropie, il s'avère que les coordonnées des deux référentiels
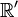

Si ces coordonnées sont celles d'un point mobile, les vitesses et accélérations
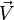
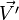
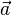
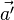

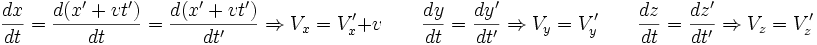
et
-
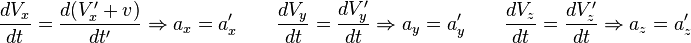
ce que l'on peut écrire vectoriellement :

Ces résultats sont les expressions de la loi de composition des vitesses de la relativité galiléenne et de la loi de conservation des accélérations lors d'un changement de référentiel galiléen.
Par ailleurs dans chacun des deux référentiels galiléens, le principe de la dynamique s'exprime comme une loi invariante lors du changement de référentiel :
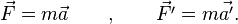
Les résultats précédents (conservation de l'accélération) amènent donc à l'identité des forces appliquées au système, forces vues de chacun des référentiels.
De plus, selon la transformation de Galilée, les vitesses s'ajoutent (V=V'+v) et ainsi aucune vitesse n'est-elle invariante lors d'une telle transformation.
Ce dernier point fut expérimentalement contredit par l'expérience de Michelson et Morley à propos de la combinaison de la vitesse de la lumière et de celle de la terre autour du soleil, dans le référentiel de Copernic.
Ce résultat troublant est expliqué dans le cadre de la théorie de la relativité restreinte.
Cependant la relativité galiléenne apparaissait incapable de mettre en évidence une invariance souhaitable des lois de l'électromagnétisme lors des changements de référentiel ; et c'est surtout ce fait qui conduisit Einstein à proposer la théorie de la relativité restreinte. Dans le cadre des transformations de Lorentz, les lois de l'électromagnétisme seront invariantes, et il existera une vitesse maximale pour toutes les interactions, identique pour tous les référentiels.
L'intervalle d'espace-temps entre deux événements
L'utilisation des deux postulats et les contraintes imposées lors des changements de référentiels vont directement mener aux relations de transformations de Lorentz (cf. ci-dessous), mais la démarche qui y mène introduit une notion extrêmement importante, l’intervalle d'espace-temps entre deux événements.
Dans un référentiel un événement est caractérisé par ses coordonnées, spatio-temporelles, " tel endroit, tel instant ". Deux événements situés respectivement en x1,y1,z1,t1 et x2,y2,z2,t2 seront séparés par un intervalle d'espace-temps dont le carré est
-
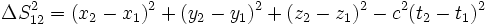
Il s'avère que cet intervalle est un invariant relativiste : sa valeur ne dépend pas du référentiel galiléen dans lequel on l'évalue. Ceci permet de classer les événements, les uns par rapport aux autres, et ce classement est absolu, ... dans le cadre de la relativité restreinte.
En particulier, des événements peuvent être ailleurs l'un par rapport à l'autre (le carré de l'intervalle d'espace-temps est positif, dans sa définition ci-dessus) ; de tels événements ne peuvent être liés par aucune interaction, ils ne peuvent être cause et effet l'un de l'autre. Dans un référentiel donné, deux événements simultanés (se passant au même instant) mais situés en deux endroits différents sont ailleurs l'un par rapport à l'autre. Lors d'un changement de référentiel, suivant les transformations de Lorentz, il apparaîtra que dans un autre référentiel, un des deux événements aura lieu à un instant antérieur à l'autre : l'ordre temporel de tels événements peut bien varier d'un référentiel à l'autre, cela n'a aucune importance : aucun n'est la source de l'autre.
Dans le cas limite où dans un référentiel deux événements ont même coordonnées, ils coïncident (l'intervalle d'espace-temps est alors trivialement nul). Cette coïncidence est alors conservée lors d'un changement de référentiel. Ceci rendra absolue la notion de choc de particules d'un référentiel dans l'autre.
Les intervalles tels que :
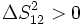
Les intervalles tels que :
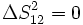
Les intervalles tels que :
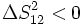
Transformations générales de Lorentz
Si les transformations spéciales simplifient l'étude analytique, elles ne nuisent en rien à la généralité. On peut aisément passer au cas où les référentiels en mouvement ne sont pas parallèles l'un à l'autre, et sont d'orientation quelconque par rapport à leur vitesse relative. Il est toujours possible de décomposer le vecteur
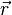
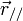
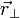
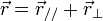
Les transformations générales de Galilée s'écrivent tout simplement :
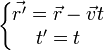
- Tandis que les transformations de Lorentz donnent :
-
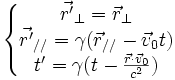
-
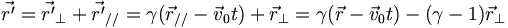
- or
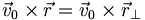
- obtenant :
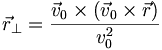
- d'où l'expression des transformations générales de Lorentz :
-
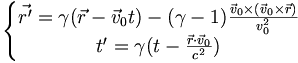
Cinématique relativiste
vitesse et accélération
Dans le cadre des transformations spéciales de Lorentz, on peut évaluer le lien entre les grandeurs cinématiques usuelles, à savoir la vitesse et l'accélération d'un point mobile, dans les deux référentiels
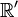

Le plus élégant est de passer en écriture quadridimensionnelle, ce qui est fait en annexe. Travaillons ici d'une façon parallèle à celle utilisée en mécanique classique. Nous supposons donc que le référentiel
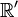
- Bien sûr les définitions doivent être identiques dans chacun des deux référentiels. Dans le référentiel

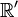
- Les relations de transformations spéciales fournissent alors en quelques lignes les expressions des composantes de la vitesse du mobile dans

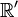
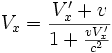
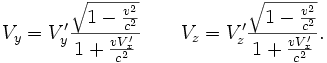
Ces relations sont remarquables à plusieurs titres :
- la loi de composition des vitesses en relativité restreinte n'est plus une loi d'addition. La vitesse limite c est bien conservée, d'un référentiel dans l'autre.
- le fait que le référentiel
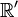
Les mêmes opérations simples fournissent les relations, compliquées, entre les composantes des accélérations du mobile dans les deux référentiels. Nous sommes alors loin de la simplicité formelle obtenue dans l'étude des transformations de Galilée. Cette simplicité est cependant retrouvée dans le cadre de la présentation quadri-vectorielle, légitime pour cette étude de l'espace temps.
vers le quadri-vecteur impulsion-énergie
En mécanique classique l'étape vers la dynamique s'effectue par l'introduction de la cinétique, c’est-à-dire l'introduction des masses dans les expressions cinématiques. Les deux grandeurs fondamentales qui intéressent les physiciens sont l'impulsion et l'énergie, grandeurs conservées pour les systèmes isolés.
En relativité restreinte, il en est de même. Cependant, il est à ce niveau très intéressant de partir d'un intervalle d'espace temps lié directement au mobile que l'on considère. L'on sait que le carré d'intervalle d'espace temps est un invariant relativiste, et ceci donne un sens tout particulier au temps propre du mobile, qui n'est autre que la racine carrée de l'intervalle d'espace-temps associé aux deux événements séparés de dx, dy, dz, cdt dans le référentiel

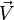

On remarque que l'expression à quatre dimensions précédente présente la caractéristique d'avoir son carré scalaire (au sens du carré d'intervalle d'espace-temps) invariante lors du changement de référentiel. Sa division par le scalaire invariant, ayant les dimensions d'un temps, tel dt0 fournit alors aussi un quadri-vecteur (de carré scalaire invariant). La multiplication par la masse m du mobile (masse sur laquelle il faudra revenir) fournit alors un quadri-vecteur dont les trois premières composantes sont reliées à ce que nous connaissons sous le terme impulsion :
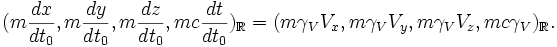
À partir des trois premières composantes l'on obtient la définition relativiste de l'impulsion, compte tenu de la relation entre le temps propre et le temps du repère :
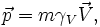
on retrouve, à la limite des faibles vitesses (
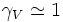
La quatrième composante, multipliée par c, présente, pour les faibles valeurs de la vitesse V, une structure très particulière :
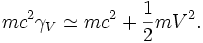
Ainsi cette quatrième composante fournit-elle l'énergie cinétique classique de cette particule de faible vitesse, augmentée par l'énergie mc2. La quantité E = mγVc2 est donc l'énergie de la particule libre, de masse m et de vitesse de module V, dans le référentiel

On peut faire plusieurs observations :
- la valeur de l'énergie totale de la particule dépend du référentiel de l'observateur. Cependant, la valeur de l'énergie de masse est identique dans tous les référentiels, et en particulier dans le référentiel propre de la particule. C'est donc une caractéristique intrinsèque de la particule. Certaines présentations de la relativité restreinte introduisent la masse variable avec la vitesse mV = mγV ; tout est affaire de convention, m est alors la masse au repos.
- lorsque V tend vers c, γV tend vers l'infini, ce qui signifie qu'il faudrait fournir une énergie infinie pour accélérer une particule jusqu'à atteindre la vitesse de la lumière. Ceci est évidemment impossible. On arrive cependant à accélérer des particules à des vitesses très proches de c.
- le carré scalaire du quadri-vecteur impulsion-énergie, invariant relativiste, a pour valeur :
- la relativité restreinte est une contrainte imposée à l'espace temps, elle est universelle et son implication apparaît dans tous les phénomènes physiques, même là où les vitesses intervenant ne sont pas relativistes. Un exemple flagrant est le défaut de masse de l'atome le plus simple : la masse de l'atome d'hydrogène
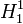
- L’équivalence de la masse et de l'énergie restera la formule célèbre gravée sur le tombeau d'Einstein :
-
Poser cette équivalence fut un pas révolutionnaire, car les concepts de matière et d'énergie étaient complètement distincts jusque là, bien que certains mathématiciens comme Poincaré ou Lorentz avaient indépendamment tenté le rapprochement dans le domaine de l'électromagnétisme.
Cette équation aurait été publiée deux ans avant le travail d'Einstein par un italien nommé Olinto De Pretto. Même si de Pretto a le premier écrit cette formule, c'est toutefois bien Einstein qui l'a rendue célèbre.
Dynamique relativiste
Principe de la mécanique relativiste
L'impulsion et l'énergie introduites ci-dessus entrent dans les expressions du principe de la dynamique, qui conserve alors une forme semblable à son correspondant classique : dans le référentiel


Une différence importante par rapport à la mécanique classique est à noter : les valeurs des composantes des forces dépendent des référentiels.
Si dans un référentiel les forces appliquées dérivent d'un potentiel U, l'énergie totale E + U est une constante. Un certain nombre de problèmes courants peuvent alors être résolus, tels, en particulier, ceux de charges dans des champs électromagnétiques. Les solutions s'obtiennent sans difficulté.
Systèmes de particules
La relativité de la notion de simultanéité mène à quelques difficultés lorsque l'on considère dans un référentiel un système comportant des particules situées en des points différents de l'espace : à un instant donné, dans ce référentiel, quelles grandeurs pouvons-nous définir sur le système, qui conserveraient un sens dans un changement de coordonnées ne conservant pas la simultanéité ?
-
- En toute rigueur donc, un solide n'existe pas en relativité ;
- considérons un simple système de deux particules chargées dont nous voulons suivre l'évolution. Dans un référentiel donné, la mise en forme des équations à résoudre est simple : deux points matériels, reliés par une simple loi de Coulomb, ceci à un instant t du référentiel

- Quelle signification accorder au quadri-vecteur somme, issu d'une transformation de Lorentz, puisque dans le référentiel

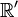
La mécanique quantique saura résoudre le problème de façon élégante en déconnectant le champ de force instantané et délocalisé en une succession d'émissions, propagations et absorptions des bosons du champ. Ainsi, en dehors des chocs entre les particules et les bosons, les particules sont libres et pour chacune d'entre elles, les valeurs de l'impulsion et de l'énergie se conservent, ce qui permet d'éliminer le problème du ou des instants des mesures.
La définition de l'impulsion-énergie du système porte donc sur des particules sans interaction. Pour un système de N particules, sans interaction, l'impulsion-énergie dans le référentiel

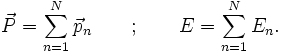
A partir de ces expressions, l'on définit le référentiel du centre de masse du système
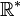
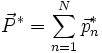
- la vitesse du référentiel de centre de masse dans le référentiel

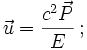
- l'énergie du système dans le référentiel du centre de masse. C'est cette énergie qui interviendra dans la balance des créations de particules, en cas de choc :
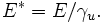
On notera que, dans ce cadre, parler du référentiel du centre de masse d'un système formé d'une particule à masse non nulle et d'une particule sans masse (par ex. photon) est possible.
Dans le cas d'un choc, l'interaction entre les particules définit une coïncidence : au même lieu, au même instant. Cette coïncidence a lieu quel que soit le référentiel de description. La conservation de l'impulsion-énergie gère les différentes possibilités, sorties du choc : choc élastique, choc inélastique.
Il est à noter que la relativité restreinte ne définit pas quels sont les produits d'un choc. Elle ne concerne que la balance impulsion-énergie. Les différentes possibilités (apparition de telle ou telle particule) seront déterminées par le type d'interaction qui interviendra entre les particules qui subissent le chocs, interaction forte, interaction faible ou interaction électromagnétique. Une autre contrainte intervient aussi : la mécanique quantique.
Électromagnétisme et relativité restreinte
Champ électromagnétique
Les équations de Maxwell sont invariantes par transformation de Lorentz ; les champs
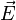
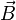
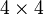
Il peut être plus simple d'introduire les potentiels vecteur
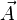
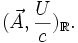
Onde électromagnétique et photons
En dehors des sources, les solutions des équations de Maxwell, peuvent s'écrire comme combinaisons linéaires d'ondes planes, de vecteur d'onde

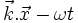
Il s'ensuit qu'est associé à l'onde plane un quadri-vecteur :
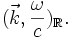
qui suit les relations de transformation de Lorentz. L'étude de cette transformation introduit deux effets importants :
-
- l'effet Doppler-Fizeau liant les fréquences d'une onde dans deux référentiels galiléens,
- l'aberration de la lumière liant les directions de propagation de l'onde dans les deux référentiels.
L'hypothèse de quantification de l'onde électromagnétique introduit au vecteur impulsion-énergie des photons constituant l'onde :
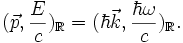
Cette quantification est nécessaire à l'explication des multiples effets d'interaction rayonnement-matière : effet photoélectrique, effet Compton, création ou annihilation de paires...
Vocabulaire
- Un observateur désigne un humain ou un appareil de détection.
- Un référentiel galiléen, appelé aussi référentiel de Lorentz ou référentiel d'inertie, est un référentiel où les observateurs ne ressentent pas d'accélération lorsqu'ils sont en mouvement rectiligne uniforme.
- Les mesures de temps sont généralement données comme des mesures de longueur, à savoir, la distance parcourue par la lumière durant le temps considéré.
- Un événement est une coordonnée de l'espace-temps, c'est-à-dire un temps et un point de l'espace dans un référentiel donné. (Il correspond à la notion commune d'événement qui se passe à moment donné en un endroit donné.)
Citations
- " La relativité nous enseigne les liens entre différentes descriptions d'une même et unique réalité. " (Einstein)
- " Si ma théorie de la relativité est avérée, l'Allemagne va prétendre que je suis un Allemand et la France dira que je suis un citoyen du monde. Si elle est réfutée, la France dira que je suis allemand et l'Allemagne me dira juif. " (attribué à Einstein)
- " Quand un homme s'assied une heure en compagnie d'une jolie fille, cela lui paraît une minute. Mais faites-le asseoir sur un poêle une minute et cela lui semblera durer plus d'une heure. C'est ça la relativité. " (Einstein, Journal of Exothermic Science and Technology, Vol.1, No.9; 1938)
- " Personne n'a encore découvert d'applications militaires à la théorie des nombres et à la relativité, il semble improbable qu'on en trouve avant pas mal d'années. " (Godfrey Harold Hardy, A Mathematician's Apology)
- " J'accepte aussi peu la théorie de la relativité que l'existence des atomes. " (attribué à Ernst Mach)
Bibliographie
Une sélection des œuvres d'Einstein, notamment ses articles originaux, sont aujourd'hui disponibles en traduction française commentée sous le titre Œuvres choisies aux éditions du Seuil/CNRS éditions, dans la collection Sources du savoir (6 volumes parus depuis 1989). Les tomes 2 et 3 sont exclusivement consacrés aux théories de la relativité.
Ouvrages de vulgarisation
- Albert Einstein ; La relativité, Gauthier-Villars (1956). Réédité par Payot (1990) ISBN 2228882542. Au format poche, un exposé élémentaire des principes de la théorie de la relativité restreinte et générale, par son auteur. Indémodable.
- Banesh Hoffmann ; Histoire d'une grande idée : la relativité, Éditions Pour La Science (1985), diffusion Belin ISBN 0-9029-1844-5. Un exposé remarquable pour sa clarté et sa simplicité de la relativité, par un ancien collaborateur d'Einstein à l'Institute for Advanced Studies de Princeton.
- Thibault Damour ; Si Einstein m'était conté, Editions du Cherche-midi, Paris (2005) ISBN 2-74910-390-8. Le grand spécialiste français des théories de la relativité nous livre enfin " son " Einstein sans équations. Thibault Damour est professeur permanent à l'Institut des Hautes Études Scientifiques (IHES) de Bures-sur-Yvette ; il a longtemps enseigné la relativité générale au DEA. de physique théorique de la rue d'Ulm.
- Albert Einstein & Leopold Infeld ; L'évolution des idées en physique, Collection Champs, Flammarion (1993) ISBN 2080811193. Au format poche, une histoire de la physique, de la Mécanique de Newton jusqu'aux théories modernes (relativité, quanta), écrite en 1936 par le Maître lui-même et l'un des ses disciples à Princeton, pour financer le séjour de ce dernier.
- Brian Greene ; L'Univers élégant, folio essais (2005) ISBN 2-07-030280-6. Livre de vulgarisation remarquable sur l'état actuel de la physique
Ouvrages d'initiation au formalisme
Accessibles au niveau premier cycle universitaire.
- James H. Smith ; Introduction à la relativité, InterEditions (1968). 2ème édition avec exercices corrigés (1979) ISBN 2-7296-0088-4. Réédité par Masson (Dunod - 3ème édition - 1997), ISBN 2225829853. Un livre en français qui expose les bases de la théorie de façon claire.
- M. Boratav & R. Kerner ; Relativité, Ellipses (1991), ISBN 2-7298-9145-5. Un très bon livre en français, écrit dans un style très vivant par deux professeurs à l'Université Paris 6. Contient de nombreux exemples et applications issus d'expériences récentes.
- E.F. Taylor & John A. Wheeler ; À la découverte de l'espace-temps, Dunod (1970). Cet ouvrage original est une introduction élémentaire, quoique rigoureuse, à la théorie de la relativité restreinte ; Wheeler est un expert incontesté du domaine. Le public visé est l'étudiant de premier cycle débutant en physique ; en particulier, la connaissance de l'électromagnétisme n'est pas nécessaire. C'est le complément idéal pour prolonger la lecture du livre de Banesh Hoffman cité ci-dessus. De nombreux exercices, dont une bonne part résolue. Malheureusement plus édité en français, cet ouvrage reste disponible en anglais : Spacetime Physics, W. H. Freeman (2ème édition - 1992), ISBN 0716723271.
- [LL77] Jean-Marc Levy-Leblond ; Les relativités, Cahiers de Fontenay n° 8, École Normale Supérieure de Fontenay-aux-Roses (1977). Notes de cours très pédagogiques, hélas non publiées. Disponibles dans les bonnes bibliothèques universitaires ...
- Max Born La théorie de la relativité d'Einstein et ses bases physiques, Gauthier-Villars (1923). Réédité par Jacques Gabay (2003) ISBN 2-87647-230-9. Cet ouvrage, écrit par un grand théoricien allemand, prix Nobel 1954, est remarquable pour sa clarté. La place occupée par l'aspect mathématique y est extrêmement réduite.
- Albert Einstein La théorie de la relativité restreinte et générale, Dunod (2005) ISBN 2100487167. La version anglaise se trouve sur le projet Gutenberg
- Albert Einstein Quatre conférences sur la théorie de la relativité, Dunod (2005) ISBN 2100492292. Texte de quatre conférences prononcées à l'université de Princeton en 1921.
- Thibault Damour & Stanley Deser ; Relativité, Encyclopeadia Universalis 19 (1995) 739-748. Un exposé non technique d'une grande clarté, par un spécialiste de notoriété mondiale : Thibault Damour est professeur permanent à l'Institut des Hautes Études Scientifiques (I.H.E.S.) de Bures-sur-Yvette ; il a longtemps enseigné la relativité générale au D.E.A. de physique théorique de Paris.
- Jean-Pierre Provost & Marie-Antoinette Tonnelat ; Espace-temps, Encyclopeadia Universalis 8 (1995) 743-745. Un exposé d'introduction assez simple, ou l'essentiel de la relativité en quatre pages .
- Hubert Lumbroso ; Relativité - Problèmes résolus, Édisciences (2ème édition-1996) ISBN 2-84074-127-X. Ouvrage classique de taupe : un résumé de cours, avec un très grand nombre de problèmes corrigés.
- Wolfgang Rindler ; Introduction to special relativity, Oxford University Press (2ème édition-1991) ISBN 0-19-853952-5. Une introduction écrite par un professeur de l'Université de Dallas (Texas), spécialiste mondial du domaine.
- N.D. Mermin ; It's about time: understanding Einstein's relativity, Princeton university press (2005), ISBN 0691122016.
- David Bohm ; The special theory of relativity, Benjamin (1965), réédité par Routeledge (Londres-1996) ISBN 0415148081. Il s'agit du cours professé au Birbeck College de l'Université de Londres par David Bohm, théoricien de la physique quantique, récemment disparu. Le formalisme mathématique est réduit au strict nécessaire permettant de discuter les idées physiques sous-jacentes. Niveau premier cycle universitaire.
- Wolfgang Rindler ; Relativity : special, general and cosmological, Oxford University Press (3ème édition-2001) ISBN 0-19-850836-0. Une introduction brillante à tous les aspects de la relativité, par un professeur de l'Université de Dallas (Texas), spécialiste mondial du domaine. Accessible dès le premier cycle universitaire.
- [RI77] Wolfgang Rindler ; Essential relativity : special, general and cosmological, Texts and Monographs in Physics, Springer-Verlag (2ème édition révisée-1977) ISBN 3-540-10090-3. Édition antérieure du livre précédent, toujours intéressante.
- George F.R. Ellis & Ruth M. Williams ; Flat & curved space-times, Oxford University Press (2ème édition-2000) ISBN 0-19-850656-2. Une autre excellente introduction à la relativité, par un expert, professeur de l'Université de Cape-Town (Afrique du Sud), et sa collaboratrice. Accessible dès le premier cycle universitaire.
- Clifford M. Will ; Tests of special relativity, Séminaire Poincaré " Einstein, 1905-2005 " (09 avril 2005). Ce texte en anglais, écrit par le spécialiste mondial des aspects expérimentaux des deux théories relativistes d'Einstein, décrit quelques tests expérimentaux de la relativité restreinte. À télécharger ici aux formats PostScript ou PDF.
- Julian Schwinger ; L'héritage d'Einstein - Les prolongements de la relativité, Collection L'univers des sciences, Bibliothèque Pour La Science (1988). Une présentation relativement simple de la théorie d'Einstein par un théoricien américain, prix Nobel de physique 1965 (avec Feynman et Tomonaga) pour la théorie de l'électrodynamique quantique. Vulgarisation de niveau premier cycle universitaire (il y a quelques équations simples).
- Lewis C. Epstein Relativity Visualized
Aspects historiques
- [DA04] Olivier Darrigol ; Faut-il réviser l'histoire de la relativité ?, La Lettre de l'Académie des Sciences 14 (Hiver 2004) 6-7. L'auteur est physicien théoricien de formation. Il travaille au laboratoire de recherches épistémologiques et historiques sur les sciences exactes et les institutions scientifiques (REHSEIS) du CNRS et de l'Université Paris VII. Le texte complet de sa mise au point est à télécharger (fr)

- Olivier Darrigol ; La genèse de la relativité, Séminaire Poincaré " Einstein, 1905-2005 " (09 avril 2005) 57-78. Ce texte en anglais, beaucoup plus complet que le précédent, contient quelques détails plus techniques. À télécharger ici aux formats PostScript ou PDF.
- Albert Einstein ; Œuvres choisies - Tome 2 : Relativités I, Seuil / CNRS Editions (1999), ISBN 2020101793.
- Albert Einstein ; Œuvres choisies - Tome 3 : Relativités II, Seuil / CNRS Editions (1999), ISBN 2020101807.
- Marie-Antoinette Tonnelat ; Histoire du principe de relativité, Nouvelle Bibliothèque Scientifique, Flammarion (1971) ASIN 2082101630. Une histoire monumentale, depuis l'Antiquité jusqu'aux théories d'Einstein. Comporte une imposante bibliographie. Même s'il contient peu d'équations, ce livre exige de l'attention de la part du lecteur. Certains passages techniques consacrés à la théorie de la relativité générale sont de niveau deuxième cycle universitaire minimum.
- Abraham Pais ; Albert Einstein - Sa vie, son œuvre, Interéditions (1993). Réédité par Dunod (2005) ISBN 2100493892. La biographie scientifique qui fait aujourd'hui autorité depuis sa parution en anglais en 1982, par un professeur de l'Université de Rockfeller qui a connu Einstein dans les dernières années de sa vie. Contenu extrêmement riche. Le niveau de certains passages techniques est celui d'un second cycle universitaire (au moins).
- Arthur I. Miller ; Albert Einstein's special theory of relativity - Emergence (1905) & early interpretation (1905-1911), Addison-Wesley (1981). Réédité par Springer-Verlag (1998) ISBN 0-387-94870-8. Une étude extrêmement érudite des premiers pas de la théorie.
- Wolfgang Pauli ; Theory of relativity, Dover Publications, Inc. (1981) ISBN 0-486-64152-X. Ce livre est une mine d'informations. Il s'agit de la réédition anglaise d'un article de revue écrit en allemand en 1921 pour l'Encyklopädie der Mathematischen Wissenschaften par un jeune théoricien autrichien, alors âgé de 21 ans, étudiant à Göttingen avec Max Born. Voilà ce qu'en dit Einstein dans une lettre adressée à Born datée du 30 décembre 1921 : " Pauli est un type épatant pour ses 21 ans ; il peut être fier de son article pour l'Encyclopédie. ".
- Françoise Balibar ; Galilée, Newton lus par Einstein - Espace & Relativité, Collection Philosophies, Presses Universitaires de France (1984) ISBN 2130434932. Réflexions historiques sur le principe de relativité, en 128 pages (format poche). Il ne s'agit pas d'un exposé de la théorie d'Einstein.
Biographies d'Einstein
- Banesh Hoffmann ; Albert Einstein, créateur et rebelle, Collection Points-Sciences, Le Seuil (1975) ISBN 2020053470. Une excellente biographie au format poche, par un ancien collaborateur d'Einstein à l'Institute for Advanced Studies de Princeton.
- Philippe Frank ; Einstein - Sa vie et son temps, Collection Les savants & le monde, Albin Michel (Paris-1950). Réédition en poche dans la collection Champs, Flammarion (1993) ISBN 2080812424. Une biographie autorisée de première main, par celui qui fut le successeur d'Einstein à la chaire de physique théorique de l'Université de Prague, nommé sur sa recommandation. Très documentée, elle décrit admirablement le contexte historique (scientifique et politique) de la genèse des travaux d'Einstein.
- Abraham Pais ; Albert Einstein - Sa vie, son œuvre, Interéditions (1993). Réédité par Dunod (2005) ISBN 2100493892. La biographie scientifique qui fait aujourd'hui autorité depuis sa parution en 1982, par un professeur de l'Université de Rockfeller qui a connu Einstein dans les dernières années de sa vie. Contenu extrêmement riche. Le niveau de certains passages techniques est celui d'un second cycle universitaire (au moins).
- Jacques Merleau-Ponty ; Einstein, Collection Champs, Flammarion (1997) ISBN 2080813382. Une autre biographie au format poche, par un professeur d'épistémologie de l'Université de Paris X - Nanterre. L'ouvrage est divisé en trois parties : l'homme, son œuvre scientifique et sa philosophie.
- Françoise Balibar ; Einstein : La joie de la pensée, collection Découvertes, Gallimard (1993), ISBN 2070532208.
Notes et références
- ↑ On peut aussi dire que cette vitesse de la lumière dans le vide ne dépend pas de la vitesse de sa source.
- ↑ J. Kunz ; American Journal of Science 30 (1910) 1313.
- ↑ D.F. Comstock ; Physical Review 30 (1910) 267.
- ↑ Le cas c2 fini négatif est exclu, car la théorie ne possèderait alors plus aucune notion de causalité.
- ↑ en http://www.annales.org/archives/x/marchal2.pdf
- ↑ (de) Albert Einstein, Zur Elektrodynamik bewegter Körper, Annalen der Physik, 17, p. 891, 30 juin 1905. [(en)lire en ligne]
- ↑ {en} http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Special_relativity.html
- ↑ " for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect".
- ↑ Le principe d'homogénéité de l'espace-temps n'est pas seulement, comme on le croit généralement, un principe d'homogénéité pour un observateur particulier mais bien un postulat sur le caractère absolu des translations d'espace-temps. La première formulation rigoureuse du principe d'homogénéité est due à V. Lalan: Si, avant d'effectuer l'opéation C [la transformation de référentiel], on change l'origine du système S, il est possible de ramener l'expression de l'opération C à sa forme primitive en effectuant un changement d'origine convenable dans le système S' , V. Lalan, Sur les postulats qui sont à la base des cinématiques, Bulletin de la S. M. F., tome 65, p.83-99 (1937). Pour une discussion plus moderne, voir L. A. Lugiato and V. Gorini, On the Structure of Relativity Groups, J. Math. Phys., Vol. 13, N°5 (1972).
- ↑ V. Berzi and V. Gorini, Reciprocity Principle and the Lorentz Transformations, J. Math. Phys., Vol. 10, N°8 (1969)