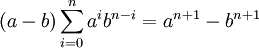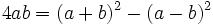Identités remarquables - Définition
En mathématiques, on appelle identités remarquables certaines égalités vraies dans tout anneau commutatif (qui doit parfois être unitaire), donc en particulier dans l'ensemble des entiers relatifs, dans l'ensemble des réels, dans l'ensemble des nombres complexes, ou dans des anneaux de polynômes. Elles servent en général à accélérer les calculs, à simplifier certaines écritures, à factoriser ou à développer des expressions.
On peut citer les plus connues, valables dans un anneau commutatif unitaire A, pour tout couple (a,b) et pour tout entier n :
- Trinôme carré parfait :
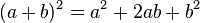
- Trinôme carré parfait :
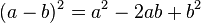
- Différence de carrés :
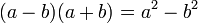
- Quadrinôme cube parfait :
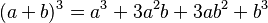
- Quadrinôme cube parfait :
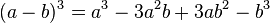
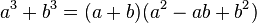
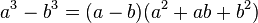
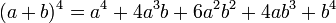
Qui se généralisent en :
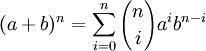
(formule du binôme de Newton)
Populaires