Application (mathématiques) - Définition
En mathématiques, une application (ou fonction) f est la donnée de deux ensembles, l'ensemble de départ E et l'ensemble d'arrivée F, et d'une relation associant à chaque élément x de l'ensemble de départ un et un seul élément de l'ensemble d'arrivée, que l'on appelle image de x par f et que l'on note f(x). On dit alors que f est une application de E dans F (noté f : E

Le terme fonction est souvent utilisé pour les applications à valeurs numériques, réelles ou complexes, c'est-à-dire lorsque l'ensemble d'arrivée est


L'image d'une application f : E

Le graphe d'une application f : E

Fonction et application
La notion de fonction en tant que correspondance entre deux types d'objet est relativement ancienne. Mais le terme n'apparait qu'à la fin du XVIIe siècle sous la plume de Leibniz en 1694[1] , il s'agit alors de fonction associée à une courbe géométrique : Leibniz dit ainsi que l'abscisse, l'ordonnée ou le rayon de courbure d'une courbe en un point M est une fonction du point M. Dans la même époque, Newton parle de fluente pour des quantités dépendant d'une variable qu'il appelle le temps (tout en précisant que le rôle joué par le temps, peut l'être par une autre quantité). La notation sous la forme f ne s'est pas mise en place tout de suite. Jean Bernoulli propose d'appeler X la fonction de x, Leibniz invente une notation permettant de travailler sur plusieurs fonctions différentes :
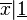
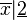
Parallèlement se développe, en géométrie, la notion d'application pour des correspondances ponctuelles.
Dans les années 1950, l'école Bourbaki tente de faire correspondre les deux notions en parlant de
- relation ou graphe fonctionnel : (E,F,G) où E et F sont deux ensembles non vides et où G est un sous-ensemble non vide de E x F vérifiant en outre, pour tous couples (x,y) et (x’,y’) de G, si x = x’ alors y = y’. (i.e. chaque élément de E possède au plus une image) ;
- application pour un graphe fonctionnel dans lequel tout élément de E possède une image.
S'appuyant sur cet embryon de distinction, les mathématiques modernes des années 1970 distinguent alors deux objets différents
- la fonction : définie par un ensemble de départ E, un ensemble d'arrivée F et une relation de E vers F dans laquelle chaque élément de E possède au plus une image. L'ensemble des éléments de E possédant une image est alors appelé domaine de définition de la fonction
- l'application : définie par un ensemble de départ E, un ensemble d'arrivée F et une relation de E vers F dans laquelle chaque élément de E possède une image et une seule
En pratique, le fait qu'il suffise de réduire l'ensemble de départ d'une fonction à son ensemble de définition pour la transformer en application rend peu utile ce distingo. Celui-ci n'a d'ailleurs jamais été adopté par la communauté mathématique dans son ensemble, qui continue à utiliser ces deux termes dans leur sens historique, i.e. le terme fonction étant utilisé comme synonyme du terme application dans le cas particulier où l'ensemble d'arrivée est


Définition
Dans la théorie de Zermelo-Fraenkel, une application de E dans F est définie comme un sous-ensemble G du produit cartésien
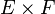
![\forall x\,\forall y\,\forall z\,\left[\left(x,y\right)\in G\wedge \left(x,z\right)\in G\rightarrow y=z\right]\,](https://static.techno-science.net/illustration/Definitions/autres/1/1d18925540868b8d2fc7990e81f0f8c2_65302785d019c2a7f0a04aea4d35d832.png)
![\forall x\,\left[x\in E\rightarrow \exists y\, \left(x,y\right)\in G\right]](https://static.techno-science.net/illustration/Definitions/autres/8/86e05538a719547a5fccc1c346b97cc5_e86524a1a00e03be0c5ffa3e0efd2030.png)
Reformulée en termes clairs, ces relations signifient exactement que G intersecte chaque sous-ensemble
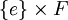
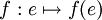
On dit que f associe à e l'élément f(e), ou encore que f envoie e sur f(e) ; ou e est envoyé par f sur f(e). La définition d'une application s'appuie donc directement sur le schéma de compréhension, mais dépend aussi de la définition du produit cartésien. Le produit cartésien s'appuie lui-même sur l'axiome de la réunion, l'axiome de l'ensemble des parties et enfin sur le schéma de compréhension.
Une application de E dans F est un élément du produit :
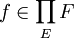
En toute généralité, l'existence d'applications intéressantes dépend de l'axiome du choix. Sans cet axiome :
- L’identité ou application identique d’un ensemble E dans lui même. Elle correspond à la diagonale du produit cartésien
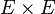
- Si E et F sont des ensembles non vides, par l'axiome de l'ensemble vide il existe au moins un élément b de F. Il est alors possible de définir une application dite application constante via la partie
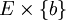
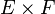
- A tout élément b de F on associe ainsi une application, l'application constante de E dans F égale à b. Cette association est une application de E dans
| ∏ | F |
| E |
.
- Si l'ensemble E est l'ensemble vide, le produit cartésien de E par F est vide ; il existe donc une unique application à valeurs dans n'importe quel ensemble.
- Par contre, si F est vide et E non vide, alors l'unique sous ensemble de
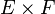
L'image d'une application f de E dans F est la collection des f(e) pour e parcourant E. C'est un sous-ensemble de F d'après le schéma de remplacement.
Opération sur les applications
- Restriction : soit E ' un sous-ensemble de E, et pour une fonction donnée comme ci-dessus par son graphe G de
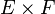
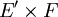
- Corestriction :
- Composition d'applications : la composition de deux applications de E1 dans E2 et de E2 dans E3 données respectivement par les graphes G1 et G2 est l'application de E1 dans E3 donnée par le graphe G suivant :
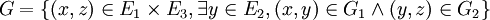
Injectivité et surjectivité
- Une application de E dans F définie par le graphe G est dite injective lorsqu'elle vérifie :
![\forall x_1\,\forall x_2\, \forall y \left[ \left(x_1,y\right)\in G\wedge \left(x_2,y\right)\in G \right] \rightarrow \left[ x_1 = x_2 \right] \,](https://static.techno-science.net/illustration/Definitions/autres/c/c094a66877c585b3c0ec6abf1068092f_a9acfb0e0283a330e6416f54ebad0452.png)
Reformulé autrement :
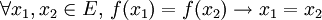
En algèbre vectoriel,une application est dite injective quand son noyau (algèbre) est réduit au vecteur nul:
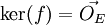
.
L'application f est aussi appelée injection ; ou encore f sépare les points de E.
- La composée de deux injections est une injection et, inversement, si go f est une injection, alors f est une injection.
- Une fonction f est dite surjective (ou que c'est une surjection , s'il s'agit d'une application) lorsque :
-
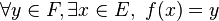
- En d'autres termes, f est surjective ssi l'image de E est l'ensemble d'arrivée tout entier; cela signifie que tout élément de l'ensemble d'arrivée peut être vu comme image d'un élément de l'espace de départ.
- La composée de deux surjections est une surjection et, inversement, si
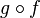
- Une application est dite bijective (ou que c'est une bijection) lorsqu'elle est à la fois injective et surjective. Attention, toutes les applications ne sont pas des bijections !
- La composée de deux bijections est une bijection mais inversement, si la composée de deux applications est une bijection, on peut seulement en déduire que l'une est une injection et l'autre une surjection.
Réciproque d'une application injective
- Si une application f : E

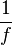
- Plus généralement, si f : E


Décomposition canonique
On appelle relation binaire associée canoniquement à la fonction f la correspondance
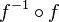
- " x est en relation avec y ssi x et y ont une image commune par f "
Cette relation est toujours symétrique et transitive, mais n'est une relation d'équivalence que si f est une application (voir l'article " Opération sur des correspondances ").
Nous pouvons alors définir l'ensemble quotient
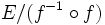
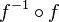
Considérons alors la correspondance i de
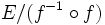
- " A est en relation avec y ssi A est l'ensemble des antécédents de y par
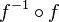
Cette correspondance est une injection, l'injection canonique associée à l'application f. On montre aisément que
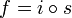
En résumé : Toute application peut être décomposée de façon unique en une surjection et une injection.
Cette décomposition est la décomposition canonique de l'application. Dans cette décomposition :
- la surjection s est une bijection ssi f est une injection, c'est-à-dire si
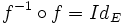
- l'injection i est une bijection ssi f est une surjection, c'est-à-dire si
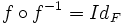
Ce qui précède peut être étendu à une fonction quelconque, à condition de " compléter " le graphe de