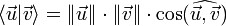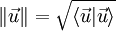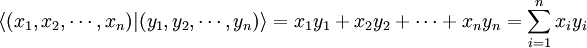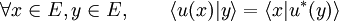Espace euclidien - Définition

Un espace euclidien, dans la conception actuelle, est un espace vectoriel ou affine réel de dimension finie muni d'un produit scalaire. Dans un tel espace, on peut traiter des questions de longueur ou d'orthogonalité. En physique, l'espace où nous évoluons est usuellement modélisé par un espace affine euclidien de dimension 3.

Première approche

L'espace euclidien tire son nom du mathématicien grec Euclide. Historiquement, l’espace euclidien est seulement l’espace physique de dimension 2 ou 3 (plan ou espace) dans lequel ont été définis les points, les droites, les distances et les angles. À ces objets ont été affectées des propriétés comme " par deux points distincts ne passe qu'une seule droite ", ou bien " la somme des angles d'un triangle vaut deux droits ".

Les transformations caractéristiques de ces espaces euclidiens sont les isométries: elles transforment des figures géométriques en d'autres figures géométriques de même dimension. Elles sont à l'origine par exemple des cas d'égalité des triangles. Les outils fondamentaux de travail dans l'espace euclidien sont la règle et le compas. Ces espaces euclidiens naturels sont les univers où sont démontrés tous les grands théorèmes de la géométrie plane ou de la géométrie dans l'espace. Ils sont les objets d'étude de tous les géomètres avant Euclide jusqu'aux mathématiciens du XIX^e siècle.

À cette date cependant, cette vision de l'espace euclidien naturel commence à montrer ses limites. Il est alors nécessaire d'en donner une définition plus formelle et plus générale . La définition du produit scalaire de deux vecteurs par

va permettre cette mutation.

Définitions mathématiques

Espace vectoriel euclidien

Un espace vectoriel euclidien est un espace vectoriel sur , de dimension finie et muni d'un produit scalaire : . On peut alors y définir une norme, appelée "norme euclidienne" :

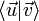
et une notion d'angle : l'angle géométrique (u,v) de deux vecteurs non nuls est le réel θ compris entre 0 et π tel que

(ce quotient est compris entre -1 et +1 d'après l'inégalité de Cauchy-Schwarz).

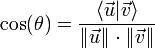
Les transformations caractéristiques de ces espaces euclidiens sont les transformations conservant le produit scalaire et la norme. Ce sont les automorphismes orthogonaux (voir groupe orthogonal).

Espace affine euclidien

Un espace affine euclidien est un espace affine associé à un espace vectoriel euclidien. On peut y définir une distance, des notions d'angle géométrique et on retrouve en particulier la propriété de Pythagore et sa réciproque ainsi que celle de la somme des angles d'un triangle.

Les transformations fondamentales des espaces affines euclidiens sont les isométries, transformations conservant les distances, on démontre que ce sont des applications affines dont l'application linéaire associée est un automorphisme orthogonal.

Exemples d'espaces vectoriel euclidien

• L'espace , muni du produit scalaire canonique

est un espace vectoriel euclidien (dit canonique) de dimension n

• L'espace vectoriel des polynômes réels de degré inférieur ou égal à n
  • muni du produit scalaire canonique

    

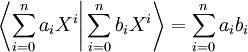
    est un espace euclidien de dimension n + 1

  • muni du produit scalaire

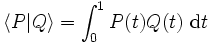
est aussi un espace euclidien dont la norme est différente de la précédente.

Propriétés des espaces euclidiens

Outre les propriétés inhérentes à la norme et au produit scalaire (voir aussi forme bilinéaire), l'espace euclidien possède des propriétés supplémentaires dues à son caractère d'espace de dimension finie.

Base

Tout espace euclidien possède une base orthonormale (chaque vecteur de la base est de norme 1, le produit scalaire de deux vecteurs différents est toujours nul). Plus précisément : si est une base de E, il existe une base orthonormale et telle que, pour tout entier k de 1 à n,

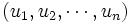
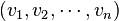
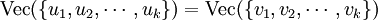
Tout espace vectoriel euclidien de dimension n est isomorphe à .

Tout espace vectoriel euclidien est complet, c'est donc un cas particulier d'espace de Banach.

Orthogonalité

Deux vecteurs dont le produit scalaire est nul sont dits orthogonaux.

À tout sous-espace vectoriel F d'un espace euclidien E on peut associer un unique sous-espace formé de tous les vecteurs orthogonaux à tous les vecteurs de F, c'est l'orthogonal de F. L'orthogonal de l'orthogonal de F est F. Un sous-espace F et son orthogonal sont supplémentaires.

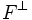
Vecteur et forme linéaire associés

L'existence de sous-espaces orthogonaux supplémentaires permet de définir la notion d'hyperplan orthogonal à un vecteur v non nul et permet de démontrer l'existence d'un isomorphisme entre E et l'ensemble des formes linéaires sur E.

Si x est un vecteur de E, l'application " produit scalaire par x " est une forme linéaire, dite associée à x.

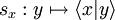
L'application qui à x associe s_x est un isomorphisme d'espaces vectoriels de E dans E ^* , espace dual de E.

Adjoint d'un endomorphisme

Si u est un endomorphisme de E, il existe un unique endomorphisme noté u ^* et appelé adjoint de u, tel que

On définit les notions d'endomorphisme autoadjoint ou symétrique (u = u ^* ), anti-autoadjoint ou antisymétrique (u = − u ^* ).

Dans une base orthonormale ou orthonormée, la matrice représentative de u ^* est la transposée de celle de u.

Notions connexes

• Un espace vectoriel sur ou sur muni d'un produit scalaire et de dimension infinie est un espace préhilbertien. L'absence de la finitude de la base lui fait perdre la liste de propriétés précitées. Si l'espace est complet c'est un espace de Hilbert.
• Un espace vectoriel sur muni d'un produit scalaire et de dimension finie est appelé espace hermitien