Espace de Cantor - Définition

On appelle espace de Cantor l'espace produit . C'est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes, totalement discontinu (on dit aussi de dimension 0), qui a la propriété universelle suivante :

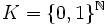
Tout espace métrisable à base dénombrable totalement discontinu est homéomorphe à un sous-espace de K.

Cela fournit en particulier un moyen commode pour compactifier les espaces métrisables à base dénombrable totalement discontinus. On en déduit que tout espace mesurable dénombrablement engendré et séparé est isomorphe à une partie de K munie de la tribu induite par la tribu borélienne de K.

L'espace de Cantor est homéomorphe à l'ensemble de Cantor, mais il est équipé naturellement d'une distance ultramétrique analogue à celle sur N^N dont on trouvera une description dans l'article " boule ". C'est aussi, en probabilité, l'espace canonique sur lequel on construit le jeu de pile ou face.

L'espace de Cantor K a la puissance du continu, et on démontre par exemple que les boréliens d'un espace métrisable compact ont la puissance du continu dès qu'ils sont non-dénombrables en prouvant qu'ils contiennent un sous-espace homéomorphe à K.