Échelle logarithmique - Définition

Une échelle logarithmique est un système de graduation sur une demi-droite [Ox), particulièrement adapté pour rendre compte des ordres de grandeur dans les applications. De plus elle permet de rendre accessible une large gamme de valeurs.

Définition de l'échelle logarithmique

L'échelle logarithmique d'une demi-droite [Ox) est déterminée par la donnée d'un point A de cette demi-droite. Pour tout point M de [Ox), les vecteurs et sont positivemennt colinéaires. Il existe donc un unique réel r tel que : . La coordonnée logartithmique de M est donnée par :

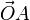
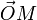
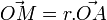
logr

En particulier, la coordonnée logarithmique de A est log(1)=0. C'est l'origine du repère.

Dans cette formule, le logarithmique peut désigner :

• En mathématiques, Le logarithme népérien, primitive de 1/x.
• En statistiques, généralement le logarithme décimal.
• En informatique, le logarithme binaire.

• La distance qui sépare 1 de 10 est la même que celle qui sépare 10 de 100 et celle qui sépare 0,1 de 1 car log(100) - log(10) = log(10) - log(1) = log(1) - log(0,1). Chacun de ces intervalles s'appelle un module.
• la distance qui sépare 1 de 2 est égale à celle qui sépare 10 de 20 mais est supérieure à celle qui sépare 2 de 3 car log(2) - log(1) = log(20) - log(10) > log(3) - log(2).

Cela induit une sorte d'irrégularité récurrente dans les graduations.

Exemple d'échelle logarithmique à trois modules

L'échelle logarithmique est une alternative à l'échelle linéaire. Elle peut s'avérer préférable pour deux raisons :

• Situation 1 : Lorsqu'on étudie un phénomène utilisant une gamme étendue de valeurs, l'échelle linéaire est mal adaptée. On lui préfère une échelle logarithmique qui espace les valeurs faibles et rapproche les valeurs fortes.

• Situation 2 : Certaines sensations suivent la loi de Weber-Fechner qui affirme qu'elles peuvent "croître comme le logarithme de l'excitant." L'échelle logarithmique donne alors un reflet fidèle de la perception subjective.

Observation graphique

Attention, à bien différencier ln et log qui permettent toutes deux de créer des échelles logarithmiques mais les calculs de pente seront différents.

Le schéma ci-dessus permet de visualiser les deux types d'échelles :

• Pour l'échelle linéaire, deux graduations dont la différence vaut 10 sont à distance constante.
• Pour l'échelle logarithmique, deux graduations dont le rapport vaut 10 sont à distance constante.

Exemples

• Magnitude d'un séisme
• pH
• Magnitude des étoiles
• Musique
• Son
• Repère semi-logarithmique, repère log-log