Commutateur (opérateur) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En mathématiques

En mathématiques, le commutateur donne une idée assez imprécise, sur la façon dont une loi n'est pas commutative. Il existe plusieurs définitions utilisées en théorie des groupes et en théorie des anneaux.

En théorie des groupes

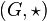
Soit $(G, \star)$ un groupe et soient $g$ et $h$ deux éléments du groupe. On appelle commutateur de $g$ et $h$ , l'élément du groupe, défini par: $[g,h]=g\star h \star g^{-1}\star h^{-1}$ .

Remarque: Un commutateur représente en fait le défaut de " permutabilité " de deux éléments du groupe.

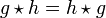
Proposition: Le commutateur est égal à l'élément neutre du groupe si et seulement si $g$ et $h$ sont permutables (c'est-à-dire si $g\star h=h\star g$ ).

D'autre part, le sous-groupe engendré par l'ensemble des commutateurs est appelé le groupe dérivé noté $D (G)$ ou le sous-groupe des commutateurs de $G$ .

Si $D (G)$ est réduit à l'élément alors le groupe $G$ est un groupe abélien.

Remarquons que nous devons considérer le sous-groupe engendré par les commutateurs parce qu'en général l'ensemble des commutateurs n'est pas fermé pour cette loi. Les commutateurs sont utilisés pour définir les groupes nilpotents.

Note: Certains auteurs préfèrent définir $g$ et $h$ par

Identités

Dans la suite, la loi $\star$ est notée multiplicativement et l'expression a^x désigne le conjugué (par x) de l'élément a c'est-à-dire x⁻¹a x.

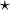
[y,x] = [x,y] ⁻¹
[[x,y⁻¹],z] ^y [[y,z⁻¹],x] ^z [[z,x⁻¹],y]^x = 1
[xy,z] = [x,z]^y [y,z]
[x,yz] = [x,z] [x,y]^z

Le deuxième identité est aussi connue sous le nom d' identité de Hall-Witt. Il s'agit d'une identité de la théorie des groupes analogue à l'identité de Jacobi de la théorie des commutateurs dans les anneaux. (Voir la section suivante.)

En théorie des anneaux

Le commutateur de deux éléments $a$ et $b$ d'un anneau ou d'une algèbre associative est défini par

[a, b] = a b - b a

Il est nul si et seulement si $a$ et $b$ sont permutables. En algèbre linéaire, si deux matrices commutent relativement à une base, alors elles commutent relativement à toute base.

En utilisant le commutateur comme un crochet de Lie, toute algèbre associative peut être considérée comme une algèbre de Lie. Le commutateur de deux opérateurs sur un espace de Hilbert est un concept important en mécanique quantique puisqu'il mesure à quel point deux descriptions d'observables par des opérateurs peuvent être mesurés simultanément. Le principe d'incertitude est finalement un théorème sur les commutateurs.

De même, l'anticommutateur est défini comme $a b + b a$ , souvent écrit noté ${a, b}$ . Voir aussi algèbre de Poisson.

Identités

Un commutateur vérifie les propriétés suivantes:

Relation d'algèbre de Lie:

[a,b] = − [b,a]
[a,a] = 0
[a,[b,c]] + [b,[c,a]] + [c,[a,b]] = 0

Relations d'addition:

[a,bc] = [a,b]c + b[a,c]
[ab,c] = a[b,c] + [a,c]b
[a,bc] = [ab,c] + [ca,b]
[abc,d] = ab[c,d] + a[b,d]c + [a,d]bc

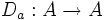
Si $a$ est un élément donné d'un anneau $A$ , la première relation d'addition peut aussi être interprétée comme la règle de dérivation d'un produit d'une application $D_a:A\rightarrow A$ donnée par $b \mapsto [a,b] \ .$ En d'autres termes, l'application D_a définit une dérivation sur l'anneau $A$ .