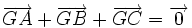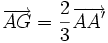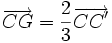Centre de gravité (mathématiques élémentaires) - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
On appelle centre de gravité d'un triangle le point d'intersection de ses 3 médianes.
Propriété : Il est situé aux

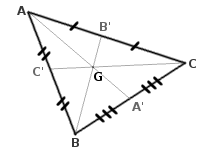
Autrement dit, soit un triangle ABC, A' le milieu de [BC], B' le milieu de [AC], et C' le milieu de [AB] et G son centre de gravité.
|
| Alors :
|
Le centre de gravité est aussi l' isobarycentre des sommets du triangle, c'est-à-dire que