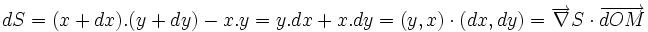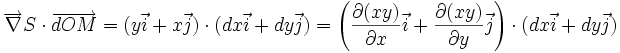Calcul infinitésimal - Définition
Le calcul infinitésimal (ou calcul différentiel et intégral) est une branche des mathématiques, développée à partir de l'algèbre et de la géométrie, qui implique deux idées majeures complémentaires:
- Le calcul différentiel est la théorie qui traite des taux de variation et fait intervenir la méthode de différentiation. En terme de fonctions mathématiques, la vitesse, l'accélération, et les pentes des courbes en un point donné peuvent toutes être décrites sur une base symbolique commune.
- Le calcul intégral, qui développe l'idée d'intégration, fait intervenir le concept d'aire sous-tendue par le graphe d'une fonction et inclut des notions connexes comme le volume.
Ces deux concepts définissent des opérations inverses au sens précis défini par les théorèmes fondamentaux du calcul infinitésimal. Ceci veut dire qu'ils ont une priorité équivalente. Cependant l'approche pédagogique habituelle commence par le calcul différentiel.
Historique
Le développement du calcul infinitésimal est attribué à Archimède, Leibniz et Newton. Cependant, lorsque le calcul infinitésimal a été initialement développé, une controverse fut soulevée sur qui en avait la paternité ; Leibniz et Newton étant les principaux candidats. La vérité ne sera probablement jamais connue et de toute façon elle importe peu de nos jours. La contribution majeure de Leibniz fut sans conteste son système de notation.
La controverse fut cependant malheureuse car elle a divisé pendant de nombreuses années les mathématiciens anglophones et ceux du reste de l'Europe. Cela a retardé le progrès de l'analyse (mathématiques basées sur le calcul infinitésimal) en Grande-Bretagne pendant longtemps. La terminologie et les notations de Newton étaient clairement moins flexibles que celles de Leibniz. Elles furent malgré tout conservées jusqu'au début du XIXe siècle lorsque le travail de l'Analytical Society introduisit avec succès la notation de Leibniz en Grande-Bretagne.
On pense que Newton a découvert plusieurs concepts bien avant Leibniz, mais que ce dernier fut le premier à les publier. Actuellement, on considère que Leibniz et Newton ont développé le calcul infinitésimal indépendamment.
Barrow, Descartes, Fermat, Huygens et Wallis contribuèrent également dans une moindre mesure au développement du calcul infinitésimal.
Kowa Seki, un mathématicien japonais contemporain de Leibniz et Newton, a aussi énoncé quelques principes fondamentaux du calcul intégral. Cependant son travail ne fut pas connu en Occident à cette époque suite au manque de contacts avec l'Extrême-Orient. (lien)
La justification première du développement du calcul différentiel était de trouver une solution du " problème de la tangente ".
Calcul différentiel
Le calcul différentiel consiste à trouver les taux de variation instantanés (ou dérivées) de la valeur d'une fonction par rapport aux variations du (des) paramètre(s) de celle-ci. Ce concept est au cœur de nombreux problèmes de physique. Par exemple, la théorie de base des circuits électriques est formulée en terme d'équations différentielles pour décrire les systèmes oscillants.
La dérivée d'une fonction permet de trouver ses extrema (minima et maxima) en étudiant ses variations. Une autre application du calcul différentiel est la méthode de Newton, un algorithme qui permet de trouver les zéros d'une fonction en l'approchant localement par ses tangentes. Ceci n'est qu'un très bref aperçu des nombreuses applications du calcul infinitésimal dans des problèmes qui à première vue ne sont pas formulés en ces termes.
Certains attribuent à Fermat la paternité du calcul différentiel.
Calcul intégral
Le calcul intégral étudie les méthodes permettant de trouver l'intégrale d'une fonction. Elle peut être définie comme la limite de la somme de termes qui correspondent chacun à la surface d'un fine bandelette sous-tendue par le graphe de la fonction. Ainsi définie, l'intégration donne un moyen effectif de calculer l'aire sous une courbe ainsi que la surface et le volume de solides comme la sphère ou le cône.
Bases
Les bases conceptuelles du calcul infinitésimal incluent les notions de fonctions, limites, suites infinies, séries infinies et continuité. Ses outils incluent les techniques de manipulation symbolique associées à l'algèbre élémentaire et l'induction mathématique. La version moderne du calcul infinitésimal est connue comme analyse réelle qui consiste en une dérivation rigoureuse des résultats du calcul infinitésimal ainsi qu'en généralisations comme la théorie de la mesure et l'analyse fonctionnelle.
Théorème fondamental de l'analyse
Le théorème fondamental de l'analyse montre que la différentiation et l'intégration sont, dans un certain sens, des opérations inverses. C'est cette " découverte " par Newton et Leibniz qui est à l'origine de l'explosion des résultats analytiques. Ce lien nous permet de retrouver la variation totale d'une fonction sur un intervalle a partir de sa variation instantanée, en intégrant cette dernière. Le théorème fondamental nous donne aussi une méthode pour calculer beaucoup d'intégrales définies de façon algébrique, sans passer réellement à la limite, en trouvant la primitive. Il nous permet aussi de résoudre certaines équations différentielles. Une équation différentielle est une équation qui lie une fonction a ses dérivées. Les équations différentielles sont fondamentales en science.
Applications
Pour rendre concrètes ces notions, considérons dans le plan (xOy) un rectangle de côté x et y. Sa surface est égale à xy et dépend des coordonnées x et y du point M. En suivant une démarche intuitive, on convient de noter par dx une très petite variation de la variable x. Lorsqu'on fait subir au point M un déplacement très faible, la surface va changer et on peut écrire que S+dS=(x+dx).(y+dy)=x.y +x.dy+y.dx + dx.dy, et on en déduit facilement que dS= y.dx+x.dy+dx.dy.
Une simple application numérique où x et y seraient des mètres et dx et dy des centimètres illustre que dx.dy est négligeable par rapport aux autres grandeurs
On peut donner un statut mathématique précis aux notations dx et dy (qui sont des formes différentielles), et à la quantité dx.dy qui est alors du second ordre. Le calcul précédent est en fait un calcul de développement limité à l'ordre 1, faisant intervenir les dérivées premières de la fonction xy par rapport aux deux variables.
On écrit donc:
Toutes ces égalités sont différentes façons d'écrire...un produit scalaire de deux vecteurs:
-
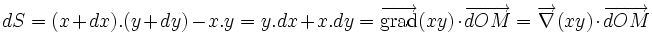
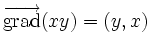
L'intérêt de l'introduction de ces vecteurs pour exprimer la variation d'une fonction de plusieurs paramètres est de visualiser le fait que la fonction va varier le plus dans la direction du vecteur gradient et qu'elle ne va pas varier pour tout changement des paramètres dans une direction perpendiculaire au gradient.
-
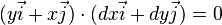
Le développement et l'utilisation du calcul infinitésimal a eu des conséquences importantes dans pratiquement tous les domaines. Il est à la base de beaucoup de sciences, notamment la physique. Presque toutes les techniques et technologies modernes font un usage fondamental du calcul infinitésimal.
Celui-ci s'est étendu avec les équations différentielles, le calcul vectoriel, le calcul des variations, l'analyse complexe, ou la géométrie différentielle.
Bibliographie
- Robert A. Adams, Calculus: A complete course. ISBN 0-201-39607-6 (1999) (en)
- Spivak, Michael, " Calculus " Publish or Perish publishing. ISBN 0914098896 (Sept 1994) (en)
- Cliff Pickover. (2003) ISBN 0-471-26987-5 Calculus and Pizza: A Math Cookbook for the Hungry Mind. (en)
- Silvanus P. Thompson and Martin Gardner, Calculus Made Easy. ISBN 0312185480 (1998) (en)
- Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7, 1986. (en)
- Calculus for a New Century; A Pump, Not a Filter. Mathematical Association of America, The Association, Stony Brook, NY. 1988. ED 300 252. (en)
- René Guénon, Les principes du calcul infinitésimal, Gallimard.