Affinité (mathématiques) - Définition
En mathématiques, en géométrie en particulier, une affinité est une application affine ou linéaire égale à l'identité dans une direction et à une homothétie dans une autre.
Affinité vectorielle
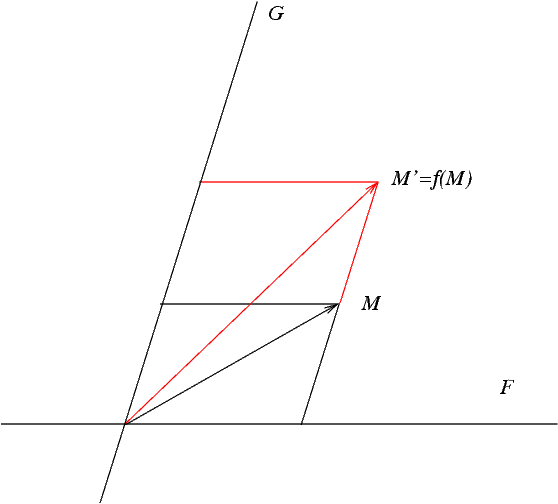
Les affinités vectorielles sont les endomorphismes qui sont somme directe de l'identité et d'une homothétie. Plus précisément :
Soit



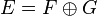
l'affinité de base








Si
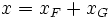
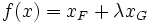
Caractérisation en dimension finie : endomorphisme diagonalisable ayant deux valeurs propre au plus dont une est l'unité.
Les affinités recouvrent :
- l'identité (
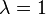
- les projections, ou projecteurs (
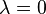
- les symétries, ou involutions linéaires (
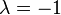
- les homothéties (
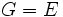
- les dilatations, ou affinités hyperplanes, (
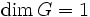
Affinité ponctuelle
Étant donné un sous-espace affine


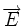
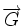


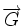
- pour tout point


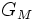

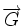
-
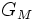


- l'image de


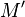
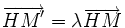
Les applications affines de partie linéaire une affinité vectorielle sont des affinités ponctuelles à condition d'avoir au moins un point fixe ; dans le cas général, on obtient des affinités glissées, composées d'une affinité et d'une translation de vecteur parallèle à la direction de l'affinité.

















































