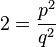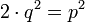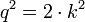Théorème - Définition
Un théorème est une proposition qui peut être mathématiquement démontrée, c'est-à-dire une assertion qui peut être établie comme vraie au travers d'un raisonnement logique construit à partir d'axiomes. Un théorème est à distinguer d'une théorie.
Une fois le théorème démontré, il est considéré comme vrai quelle que soit la valeur de vérité de sa prémisse (hypothèse de base) car il se présente sous la forme d'une implication: si A est vraie alors B est nécessairement vraie. Il peut alors être utilisé pour démontrer d'autres propositions. Démontrer le théorème consiste à démontrer l'imposssibilité d'avoir à la fois A vrai et B faux.
Un théorème a généralement :
- des hypothèses de base, i.e. des conditions qui peuvent être énumérées dans le théorème ou décrites d'avance,
- une conclusion, i.e. une affirmation mathématique qui est vraie sous les conditions de base.
La démonstration, bien que nécessaire à la classification de la proposition comme " théorème ", n'est pas considérée comme faisant partie du théorème.
Autre définition possible d'un théorème : " un énoncé dont on peut démontrer l’exactitude. "
La démonstration comprend :
- des axiomes ou des postulats ;
- les hypothèses du théorème ;
- d'autres théorèmes déjà démontrés.
Chaque étape de la preuve est liée aux précédentes par des règles d'inférence logiques.
Exemples de démonstrations
Irrationalité de la racine carrée de 2
Une démonstration par l'absurde considérée comme l'une des plus belles par Paul Erdös est la démonstration de l'irrationalité de

Par l'absurde, supposons donc que

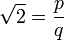
Quitte à simplifier par le PGCD de p et q, on peut supposer p et q premiers entre eux (la fraction p / q est dite irréductible).
En élevant au carré les deux membres, on obtient :
En multipliant par q2 les deux côtés, on trouve alors :
On en déduit que 2 divise p2=p×p et d'après le lemme de Gauss, puisque 2 est premier, il en résulte que 2 divise p, donc il existe k un entier tel que p=2k. On trouve alors en simplifiant par 2 :
Cette égalité montre, d'après le lemme de Gauss, que 2 divise q.
On a donc montré que 2 divise p et q, ce qui est contradictoire avec l'hypothèse de départ, où l'on avait supposé p et q premiers entre eux. CQFD.
Théorèmes de géométrie
Dans son ouvrage " Grundlagen der Geometrie " David Hilbert donne une nouvelle forme à la géométrie et en pose ses fondements.
Rappelons quelques-uns des axiomes des fondements de la géométrie :
- I, 3 Sur une droite, il y a au moins deux points ; il existe au moins trois points non alignés.
- II, 2 Deux points A et C étant donnés, il existe au moins un point B appartenant à la droite AC et tel que B soit entre A et C.
- II, 3 De trois points d'une droite, il n'y en a pas plus d'un qui se trouve entre les deux autres.
- II, 4 Soient A, B et C trois points non alignés et a une droite du plan ABC qui ne passe par aucun des points A, B et C ; si la droite a passe par l'un des points du segment AB, alors elle passe ou par un point du segment BC ou par un point du segment AC.
Démontrons le second théorème :
- Théorème
- Deux points A et C étant donnés, il existe sur la droite (AC) au moins un point D situé entre A et C (c’est-à-dire sur [AC]).
- Démonstration
- Considérons la droite AC, d'après l'axiome I, 3, il existe au moins un point E extérieur à cette droite AC. D'après l'axiome II, 2, sur la droite AE il existe au moins un point F tel que E soit compris entre A et F autrement dit tel que E soit un point du segment AF. D'après le même axiome, sur la droite FC, il existe au moins un point G tel que C soit sur le segment FG. D'après II, 3, le point G est donc extérieur au segment FC (sinon C et G sont deux points situés entre F etG). D'après l'axiome II, 4 la droite EG coupe forcément le segment AC en un point D. c.q.f.d.
D'autres formes d'assertions
Au sens large toute assertion effectivement démontrée peut prendre le nom de théorème. Dans les ouvrages de mathématiques, il est cependant d'usage de réserver ce terme aux affirmations considérées comme particulièrement intéressantes ou importantes. Selon leur importance ou leur utilité, les autres assertions peuvent prendre des noms différents :
- lemme : assertion servant d'intermédiaire pour démontrer un théorème plus important ;
- corollaire : résultat qui découle directement d’un théorème prouvé ;
- proposition : résultat relativement simple qui n'est pas associé avec un théorème particulier ;
- remarque : résultat intéressant ou conséquence qui peut faire partie de la preuve ou d'une autre affirmation ;
- conjecture : proposition mathématique dont on ignore la valeur de vérité. Une fois prouvée, une conjecture devient un théorème.
Comme énoncé ci-dessus, un théorème exige un raisonnement logique basé sur des axiomes. Cela consiste en une série d'axiomes fondamentaux (voir système d'axiomes) et un procédé d'inférence qui permet de dériver les axiomes en de nouveaux théorèmes et d'autres théorèmes démontrés auparavant. Dans la logique des propositions, n'importe quelle affirmation démontrée est appelée un théorème.