Trajectoire parabolique - Définition

Une trajectoire est dite parabolique si le mouvement d'un corps dans l'espace décrit une parabole.

La découverte de la trajectoire parabolique est attribuée à Galilée en 1638. Certains historiens des sciences pensent qu'il a été largement influencé par les artistes de son époque qui savaient représenter la trajectoire de l'eau des fontaines.^[1]

Exemples

Lorsqu'on lance un objet en l'air, hormis le cas où il a été lancé rigoureusement à la verticale vers le haut, sa trajectoire est une courbe que l'on peut assimiler à une parabole. Par exemple, le tir d'un boulet de canon ou d'une boule de pétanque décrit une trajectoire quasi-parabolique. Les comètes passent au voisinage du Soleil ou de la Terre sur une orbite " parabolique ". Si un avion effectue une trajectoire parabolique, alors les passagers embarqué se trouvent en impesanteur.

Étude de la trajectoire d'un projectile

Le mouvement d'un objet soumis à un champ de pesanteur uniforme (en l'absence de frottements) est une trajectoire parabolique (balistique).

On se place dans un référentiel R(O,x,y,z) galiléen contenant un champ de pesanteur uniforme . On se propose d'étudier la trajectoire d'un projectile M, de masse m soumis initialement (à t=0) à une vitesse .

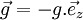
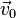
Alors, le projectile est uniquement soumis à son propre poids (on néglige les effets de frottements fluides). D'après la seconde loi de Newton, le principe fondamental de la dynamique, la somme des forces appliquées au système est égale à la masse du projectile mutlipliée par son accélération :

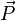
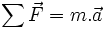
Or ici le seule force appliquée est la pesanteur, d'où :

, ou encore : .

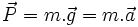
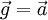
Dans le cas d'une chute libre, l'accélération de tout objet, que l'on peut considérer comme ponctuel, a pour accélération, l'accélération de la pesanteur.

Rappel : l'accélération est définie comme la dérivée au cours du temps de la vitesse, elle-même comme la dérivée au cours du temps du vecteur position. On a

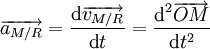
On obtient .

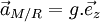
En intégrant on obtient .

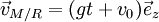
En intégrant une seconde fois on obtient puisque à l'origine, le point M est en O, ou encore, en notation vectorielle .

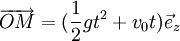
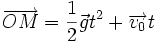
On obtient ainsi l'équation du mouvement du point M au cours du temps.

Notes et références de l'article