Pendule cycloïdal - Définition

Le pendule cycloïdal est le mouvement d'un petit anneau glissant sans frottement sur une cycloïde concave ayant pour base l'axe horizontal Ox et suivant l'équation :

avec u variant de 0 à 2π pour avoir une arche complète.

Sur cette courbe, la perle exécute, quelles que soient les conditions initiales (pourvu qu'elle reste dans l'arche), une oscillation sinusoïdale telle que la pulsation satisfasse l'égalité suivante :

• .

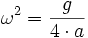Histoire des sciences

Christiaan Huygens, mathématicien du XVII^e siècle, est celui qui démontra cette formule de chute ralentie, alors qu'il ne connaissait pas le principe fondamental de la dynamique de Newton, mais seulement celui de Torricelli. Le brouillon de sa démonstration (vers 1651 ?) met en évidence l'opiniâtreté déployée pour vaincre ce problème. Il avait bien sûr remarqué que le cercle osculateur au fond du vase était de rayon 4a. Il avait également constaté que la développée de la cycloïde était la cycloïde déduite de la première par la translation .

Huygens est le créateur de la théorie concernant la développée de la développante. Celle-ci est la version géométrique précédant, de 30 ans, le célèbre théorème du calculus (le calcul différentiel et intégral) que mettront au point Newton et Leibniz : la dérivée de la primitive est la fonction elle-même.

Mais il avait remarqué aussi que le cercle montait trop lentement provoquant l'anharmonicité des grandes amplitudes (pendule pesant). Il fallait donc accentuer la pente. Il savait même qu'il faudrait (résultat peut-être déjà connu de Torricelli)

Démonstration

Lemme géométrique :

On calcule l'abscisse curviligne  :

,

d'où  ;

mais si l'on choisit l'origine au bas de la cycloïde.

Appliquer alors la formule de Torricelli :

Elle se simplifie par (loi de Galilée : tous les corps ont même loi de chute), et elle se réécrit grâce au lemme :

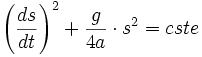 : équation de l'oscillateur harmonique.

Pratique

Découper dans du contreplaqué de 8 mm, 4 flasques de demicycloïdes ; les placer deux à deux en regard, dans deux plans parallèles, distants de 10 cm (réglable). Fixer une suspension bifilaire qui s'enroulera sur le bord curviligne des demi-cycloïdes,et y mettre un plomb. Si vous avez pris 4a = 1 m , vous aurez une superbe horloge marquant les secondes à chaque passage de verticale, même s'il y a un léger amortissement [Remarque: ce n'est pas tout à fait vrai, car la pseudopulsation, elle, dépend de l'élongation, vraisemblablement comme ]. Voir aussi puits de potentiel.

L'enregistrement des tops de passage est grandiose de régularité calme : avec un plomb de 2 kg, l'horloge ne va pas faillir avant un long moment.

Ce procédé préconisé pour les horloges à pendule est utilisé pour certaines horloges franc-comtoises, mais, dans la réalité, le feuillard qui soutient le pendule n'est pas sans rigidité : il faudrait donc revoir la théorie ; par ailleurs, le dispositif n'est guère utile depuis qu'avec le réglage d'Airy, les horloges à poids oscillent toujours à la même amplitude. Le procédé n'a donc plus guère qu'un intérêt mathématique et historique !

Géométrie

Afin de pouvoir comparer pendule simple et pendule cycloïdal , Greenhill ( ellpitic functions,1892) propose une construction via le cercle générateur (de rayon a) de la cycloïde.

Soit A, le point le plus bas de la cycloïde et le cercle (C) de diamètre vertical AE = 2a.

Soit le cercle (C1) de diamètre vertical AH = h , la perle remontant à l'altitude maximale h, niveau zéro compté en A. La droite horizontale passant par H coups la cycloïde en deux points symétriques B et B' , représentant l'élongation maximale.

Si , à un moment t, la perle P se trouve à la distance curviligne AP = s , on sait que la tangente PT = s/2.

La droite horizontale passant par P coupe OH en N , (C1) en Q et (C) en R . Démontrer que la vitesse de Q sur (C1) est constante : angle (DA,DQ) = nt , ceci quel que soit AH = h : les oscillations sont donc isochrones.

Le même genre de figure tracé pour le pendule simple fait saisir la différence et marque son amplitude par u := am(t) qui n'est plus proportionnelle à t : le pendule simple est an-isochrone.

Symétrie de Corinne

On peut poursuivre l'analogie avec le pendule simple en considérant l'ovale fermé par l'arche de la cycloïde symétrique par rapport à l'axe x'Ox : alors le mouvement est simplement donné en remplaçant t réel par it, ce qui change g en -g (cf symétrie de Corinne) ! ; donc les cos en cosh etc. Les calculs s'ensuivent très aisément. Si l'énergie E en A vaut mg .4a , la perle arrivera en O en un temps infini ; et si E > 4mga , il y aura tournoiement. Il est intéressant de comparer les plans de phase du pendule circulaire et du pendule en ovale cycloïdal.