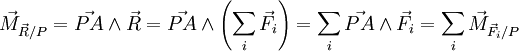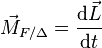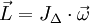Moment de force (mécanique) - Définition
En mécanique, le terme moment peut désigner plusieurs grandeurs physiques souvent liées à la considération d'un solide :
- les moments de force, moment de flexion, moment de torsion et moment d'encastrement, sont des efforts.
- le moment d'inertie représente la répartition des masses d'un solide autour d'un axe.
- le moment angulaire est lié à la notion de quantité de mouvement
- le moment dynamique est lié à la notion de quantité d'accélération.
- le vecteur vitesse d'un point d'un solide, est le moment du torseur cinématique.
Moment d'une force
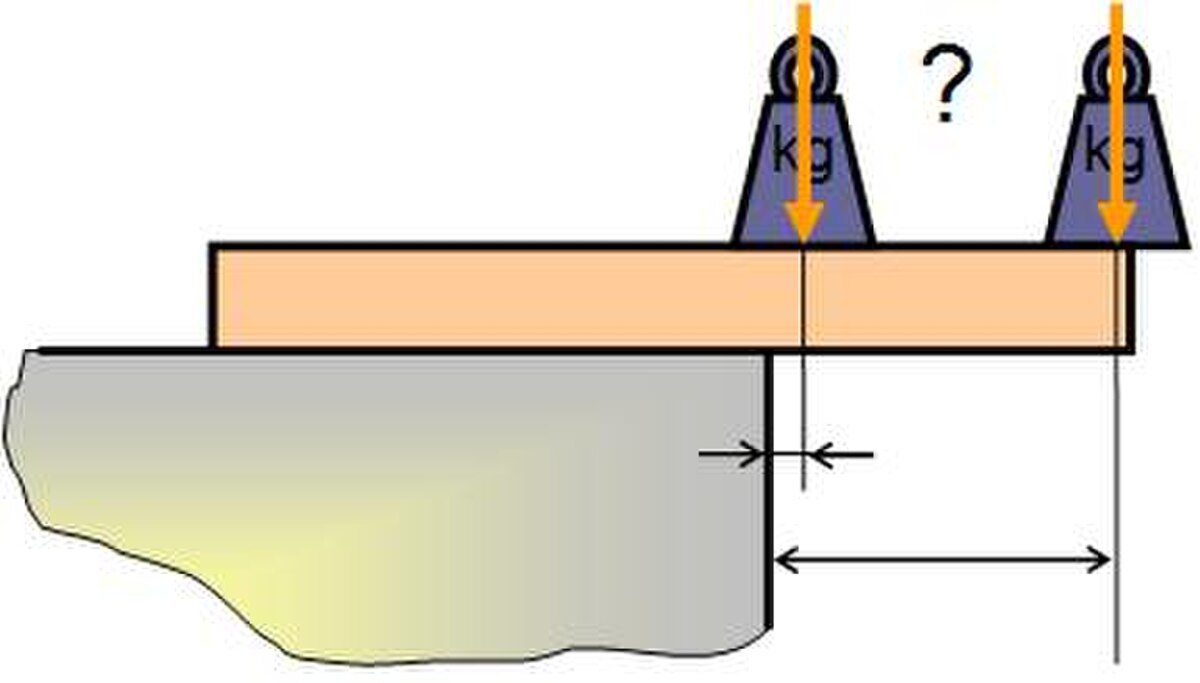
Prenez une planche en équilibre au bord d'un muret. Pour la déséquilibrer on peut poser une charge sur la partie en porte-à-faux. La capacité de cette charge à faire basculer la planche n'est pas la même suivant qu'elle est posée près du muret ou au bout de la planche. De même, on peut au même endroit, placer une charge plus grosse et constater la différence de comportement.
Le pouvoir de basculement dépend donc de l'intensité de la force, mais aussi de la position relative du point d'application et du point de rotation réel ou virtuel considéré.
Ces distinctions sont représentables par le modèle de moment d'une force qui est l'aptitude d'une force à faire tourner un système mécanique autour d'un point donné, qu'on nommera aussi pivot.
Moment par rapport à un point
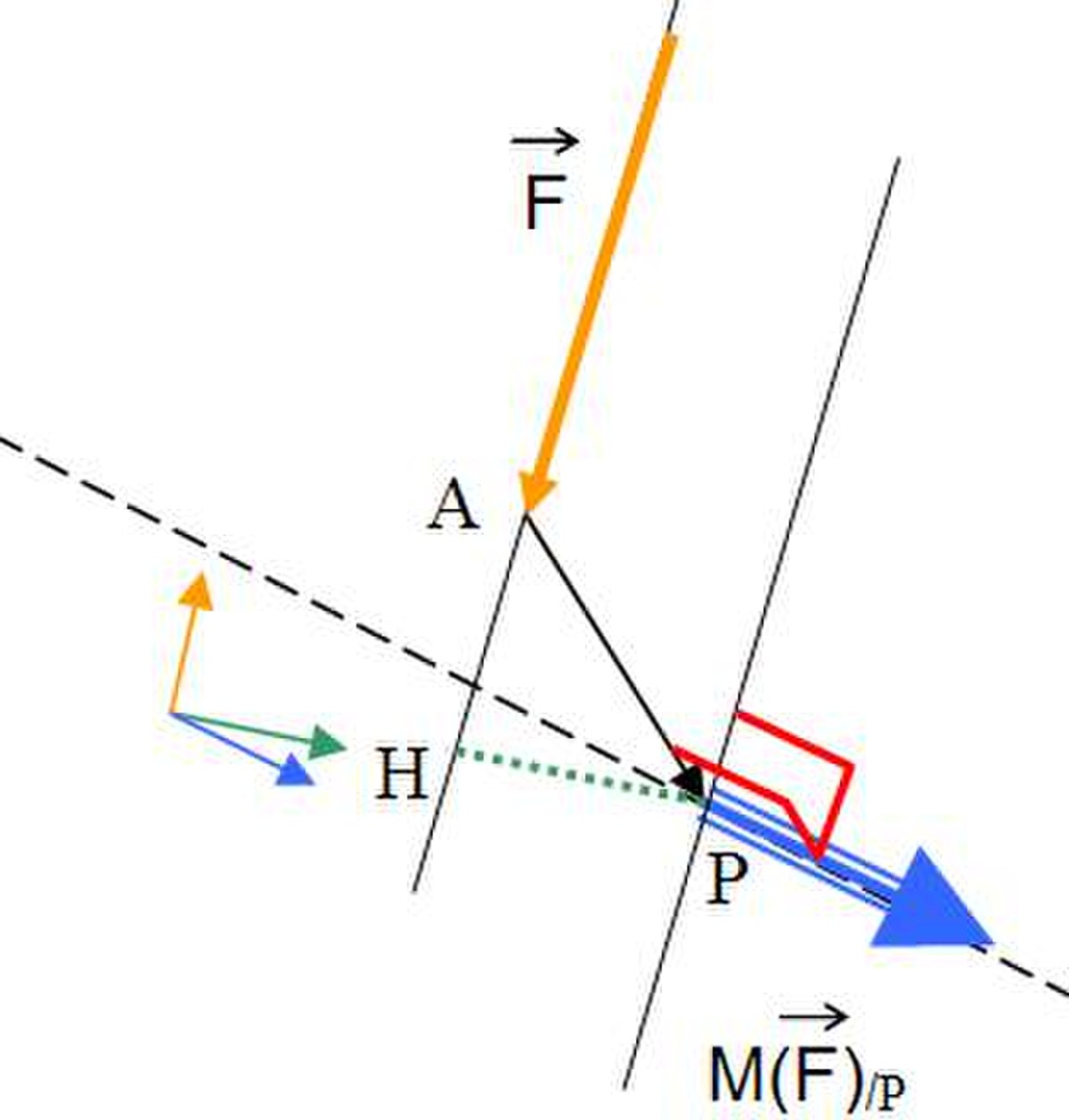
Expression vectorielle
Le moment d'une force
-
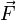
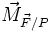
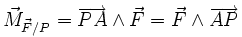
où
- Remarque sur la notation
- il existe plusieurs variantes de notation des moments de force; certaines (comme sur l'image ci-contre) comportent des parenthèses autour du vecteur, parfois autour de l'ensemble. D'autres ajoutent même à la notation l'élément agissant et l'élément subissant l'action. Une notation plus compacte consiste à nommer la force par la même lettre que celle désignant le point d'application, ce qui rend plus rapide l'identification des cas de nullité de moments.
Ce vecteur est à la fois orthogonal à
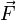
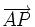
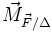
Si d est la distance orthogonale du pivot P à la droite d'action, c’est-à-dire PH, alors sa norme vaut :
-
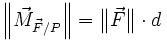
La longueur d est appelée bras de levier.
Les composantes et la norme d'un moment de force sont exprimées en Newton-mètres (Nm), dans le système international d'unités.
Cas de nullité du moment
Puisqu'il s'agit ensuite d'établir la somme nulle des moments, on peut naturellement s'intéresser aux cas de nullité individuelle des moments de force; de par les propriétés du produit vectoriel:
- la force est nulle;
- le bipoint
-
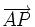
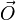
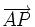
Formule de transport du moment
Lorsqu'on connaît le moment d'une force en un point, il est possible de le recalculer en n'importe quel point de l'espace. Cette opération est inévitable lorsqu'on manipule les torseurs d'actions mécaniques. Cela revient à poser une rallonge au levier AP. On montre alors la relation suivante:
-
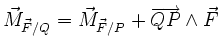
On peut vérifier alors:
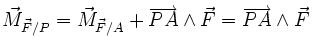
En réalité une force est modélisée par un vecteur (représentant la force) et son point d'application. Il est possible de représenter cette action mécanique par le couple de vecteurs force et moment en un point, qui sont les éléments de réduction du torseur d'action mécanique. La relation d'équilibre liée au principe fondamental de la statique devient une somme de torseurs ; en pratique, on effectuera parallèlement la somme des forces, et la somme des moments tous exprimés au même point, d'où l'intérêt de la formule de transport de moments.
Moment par rapport à un axe
Lorsqu'un solide est animé d'un mouvement de rotation effectif autour d'un axe (cas d'une roue guidée par un palier) il est intéressant de ne considérer que la part utile du moment d'une force. On définit le moment de la force par rapport à l'axe (Δ) par
-
![M_{\vec{F}/\Delta} = \vec{M}_{\vec{F}/P} \cdot \vec{u} = \left(\overrightarrow{PA} \wedge \vec{F}\right) \cdot \vec u = \left[\overrightarrow{PA}, \vec F, \vec u\right]](https://static.techno-science.net/illustration/Definitions/autres/6/606e3abbb3727190c4fab7b2be3a37ce_647a7e2d14471479838fb56e6eb646e5.png)
![M_{\vec{F}/\Delta} = \vec{M}_{\vec{F}/P} \cdot \vec{u} = \left(\overrightarrow{PA} \wedge \vec{F}\right) \cdot \vec u = \left[\overrightarrow{PA}, \vec F, \vec u\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/606e3abbb3727190c4fab7b2be3a37ce_647a7e2d14471479838fb56e6eb646e5.png)
où
En résumé il s'agit de la composante suivant
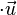
Le moment par rapport à l'axe est nul si
- le moment par rapport au point est nul (cas général précédent).
- la force est dans la direction de l'axe considéré.
Couple de forces
Si on considère deux forces opposées
- .
On remarque que le résultat est indépendant du point de pivot P considéré. Cette quantité
Outre les autres cas évidents, le couple est nul lorsque les deux forces ont la même droite d'action. Le couple augmente avec l'intensité commune des forces, mais aussi avec l'éloignement des points. Il est optimal lorsque
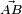
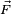
Cas général
En réalité le couple n'existe pas intrinsèquement. Il est toujours associé à un ensemble de forces s'annulant vectoriellement mais dont les moments s'ajoutent sans s'annuler. C'est par exemple le résultat de l'action du vent sur une éolienne, ou l'action des forces électromagnétiques sur l'induit d'un moteur électrique.
On ne doit donc pas faire le raccourci " somme des moments = moment de la somme ". Cela n'est vrai que pour un ensemble de forces appliquées au même point. Cela montre enfin qu'une action mécanique n'est pas représentable par un seul vecteur force. La considération du point d'application est primordiale.
Théorème de Varignon
Le moment en P de la résultante
-
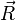
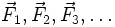
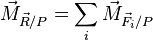
avec
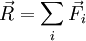
En effet :
En dynamique
En mécanique dynamique, on peut montrer que le moment des forces est la dérivée du moment cinétique par rapport au temps :
Ceci est l'équivalent du principe fondamental de la dynamique (deuxième loi de Newton) en rotation.
On peut aussi montrer que si
- colinéaire à l'axe de rotation Δ,
- dont la norme est la vitesse angulaire
- et orienté de façon que l'orientation positive d'un plan normal correspond au sens de rotation, alors :
où JΔ est le moment d'inertie du solide par rapport à l'axe de rotation Δ.
