Lagrangien - Définition
Le lagrangien
![\mathcal{L}[\varphi_i]](https://static.techno-science.net/illustration/Definitions/autres/b/b9c3f5e4b34fb0ba13145ec0678fb4d3_0d96029bf6d1d17aca907479493ef72f.png)
avec l'action
![\mathcal{S}[\varphi_i] = \int{\mathcal{L}[\varphi_i(s)]{}\,d^ns},](https://static.techno-science.net/illustration/Definitions/autres/6/6d1ddad9e9382dec25e2d70071bb51e5_68b4e8d30c0281cf71504c9b8043e195.png)
et
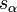
Les équations du mouvement obtenues sont équivalentes aux équations d'Euler-Lagrange. Un système dynamique dont les équations du mouvement peuvent s'obtenir à partir d'un principe de moindre d'action et d'un lagrangien est un système dynamique lagrangien. C'est le cas de la version classique du modèle standard, des équations de Newton, des équations de la relativité générale ,et de problèmes purement mathématiques comme les équations des géodésiques ou le problème de Plateau.
Un exemple en mécanique classique
Le concept de lagrangien fut historiquement introduit dans une reformulation de la mécanique classique, la mécanique lagrangienne. Dans ce contexte, le lagrangien vaut généralement l'énergie cinétique ôtée de l'énergie potentielle :
-
-
-
-
-
- L = T − V
-
-
-
-
En coordonnées cartésiennes
Le lagrangien d'une particule de masse m non relativiste dans un espace Euclidien à trois dimensions s'écrit :
où la dérivation temporelle est notée par un point au dessus de la quantité différentiée. Les équations d'Euler-Lagrange s'écrivent :
L'indice i = 1, 2, 3. Le calcul des dérivées donne :
Les équations d'Euler-Lagrange s'écrivent donc explicitement :
soit sous forme vectorielle :
Les approches lagrangienne et newtonienne sont donc équivalentes lorsque la force dérive d'un potentiel :
puisque la formulation de la deuxième loi de Newton dans un référentiel Galiléen s'écrit :
En coordonnées sphériques
Soit un espace à trois dimensions en coordonnées sphériques (r,θ,φ), et le lagrangien :
Les équations d'Euler-Lagrange s'écrivent alors :
Ici l'ensemble des paramètres
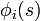
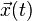
Lagrangiens et densités de lagrangien dans la théorie des champs
Dans la théorie des champs, on distingue parfois le lagrangien L, dont l'intégrale sur le temps est l'action :
et la densité lagrangienne
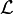
Le lagrangien est ainsi l'intégrale spatiale de la densité lagrangienne. Cependant, on appelle souvent
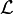
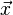
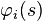
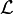
Lagrangien électromagnétique
En général, en mécanique lagrangienne, le lagrangien vaut:
- L = T − V
où T est l'énergie cinétique et V l'énergie potentielle.
Etant donnée une particule chargée électriquement de masse m et charge q, et de vitesse

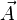
et son énergie potentielle est:
où c est la vitesse de la lumière.
Le lagrangien électromagnétique est alors:
Lagrangiens en théorie quantique des champs
Le lagrangien de Dirac
La densité lagrangienne pour un champ de Dirac est:
où ψ est un spineur,
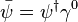
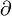
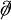
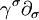
Le lagrangien de l'électrodynamique quantique
La densité lagrangienne en QED est:
où Fμν est le tenseur électromagnétique.
Le lagrangien de la chromodynamique quantique
La densité lagrangienne en QCD est (lien) (lien) (lien)
où
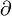
Formalisme mathématique
Soit M une variété de dimension n, et une variété de destination T. Soit
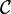
Avant tout donnons quelques exemples :
- En mécanique classique, dans le formalisme d'Hamilton, M est le variété de dimension 1

- Dans la théorie des champs, M est la variété espace-temps et l'espace de destination est l'ensemble des valeurs possibles des champs en chaque point. Si par exemple il y a m champs scalaires réels φ1,...,φm, alors la variété de destination est
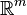

Supposons maintenant qu'il existe une fonctionnelle
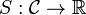


Pour que l'action soit locale, nous avons besoin de restrictions supplémentaires sur l'action. Si
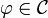
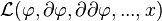
La plupart du temps, on impose que le lagrangien dépende uniquement de la valeur des champs, de leur dérivées premières, mais pas des dérivées d'ordre supérieur. C'est en fait seulement par commodité, et ce n'est pas vrai en général. Nous le supposons cependant dans le reste de cet article.
Fixons des conditions aux limites, essentiellement la donnée de φ aux frontières si M est compact, ou une limite pour φ quand x tend vers l'infini (ce qui est être pratique lors d'intégrations par parties). Le sous-espace de
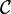
La solution est donnée par les équations d'Euler-Lagrange (en utilisant les conditions aux limites) :
Notons qu'on retrouve la dérivée fonctionnnelle par rapport à φ de l'action dans le membre de gauche.
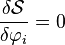
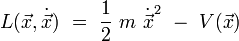
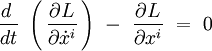
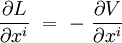
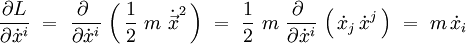
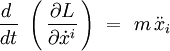
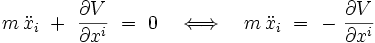
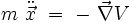
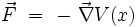
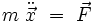
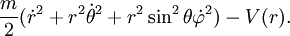
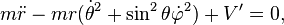
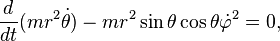
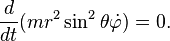
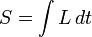
![S [\varphi_i] = \int{\mathcal{L} [\varphi_i (x)]\, d^4x}](https://static.techno-science.net/illustration/Definitions/autres/e/e4f526bbf4b6bda0d1d694eadd7675c9_18163e673b1d2120b02067ebf2dca2a1.png)
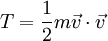
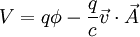
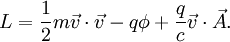
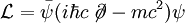
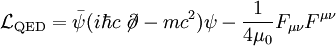
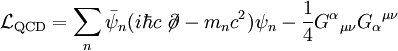
![\forall\varphi\in\mathcal{C}\, S[\varphi]\equiv\int_M d^nx \mathcal{L}(\varphi(x),\partial\varphi(x),\partial\partial\varphi(x), ...,x).](https://static.techno-science.net/illustration/Definitions/autres/8/8842702deb6e823fd032233b7638c950_9644eed6a1165211cfc747fb9a648f1c.png)