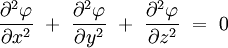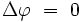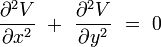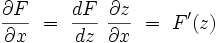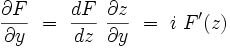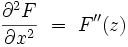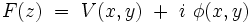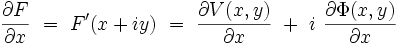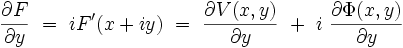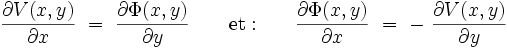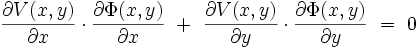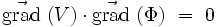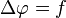Équation de Laplace - Définition

Article d'analyse vectorielle
Objets d'étude
Champ vectoriel	Champ scalaire
Équation aux dérivées partielles
de Laplace – de Poisson
Opérateurs
Nabla	Gradient
Rotationnel	Divergence
Laplacien scalaire	Bilaplacien
Laplacien vectoriel	D'alembertien
Théorèmes
de Green	de Stokes
de Helmholtz	de flux-divergence
du gradient	du rotationnel

En analyse vectorielle, l'équation de Laplace est une équation aux dérivées partielles du second ordre, dont le nom est un hommage au physicien mathématicien Pierre-Simon Laplace.

Introduite pour les besoins de la mécanique newtonienne, l'équation de Laplace apparait dans de nombreuses autres branches de la physique théorique : astronomie, électrostatique, mécanique des fluides, propagation de la chaleur, diffusion, mouvement brownien, mécanique quantique.

Toute fonction solution de l'équation de Laplace est dite harmonique.

Equation de Laplace à trois dimensions

En coordonnées cartésiennes dans un espace euclidien de dimension 3, le problème consiste à trouver toutes les fonctions à trois variables réelles qui vérifient l'équation aux dérivées partielles^[1] du second ordre :

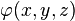
Pour simplifier l'écriture, on introduit un opérateur différentiel noté Δ et appelé opérateur de Laplace, ou simplement laplacien, tel que l'équation aux dérivées partielles précédente s'écrive de façon compacte :

Equation de Laplace à deux dimensions

En coordonnées cartésiennes dans un espace euclidien de dimension 2, le problème consiste à trouver toutes les fonctions à deux variables réelles V(x,y) qui vérifient :

On montre que toute fonction holomorphe donne des solutions de l'équation de Laplace à deux dimensions par leur partie réelle et par leur partie imaginaire ; de plus, ces solutions sont orthogonales en tout point.

Rappels sur les fonctions holomorphes

Toute fonction polynomiale à coefficients complexes est holomorphe sur  ; aussi le sont les fonctions trigonométriques et la fonction exponentielle. (Les fonctions trigonométriques sont en fait relativement proches de la fonction exponentielle puisqu'elles peuvent être définies à partir de celle-ci en utilisant les formules d'Euler).

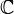
• La fonction logarithme est holomorphe sur l'ensemble des nombres complexes privé de la demi-droite des réels négatifs (on peut choisir une demi-droite quelconque issue de 0 ).

• La fonction racine carrée peut être définie par

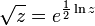
et est ainsi holomorphe partout où la fonction logarithme l'est.

• La fonction inverse est holomorphe sur .

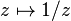
• Les fonctions trigonométriques réciproques ont de la même manières des coutures et sont holomorphes partout sauf aux coutures.

Équation de Laplace & fonctions holomorphes

Théorème 1

Démonstration

On introduit la variable complexe :z = x + iy où , et on définit la fonction holomorphe F(z). Par dérivation , on obtient que :

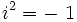
alors que :

.

En dérivant une seconde fois, on obtient d'une façon similaire :

alors que :

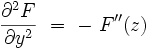
La somme est nulle, donc la fonction holomorphe F est bien une solution de l'équation de Laplace :

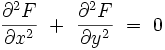
Remarque : la fonction holomorphe admet toujours une décomposition en partie réelle et partie imaginaire :

En annulant la partie réelle et la partie imaginaire séparément, on obtient deux équations de Laplace indépendantes :

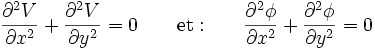
Théorème 2

Démonstration

On peut écrire :

et :

On en déduit :

soit finalement :

On reconnait là le produit scalaire des deux vecteurs :

On en déduit que les courbes à {V(x,y) = constante} et {φ(x,y) = constante} sont perpendiculaires (transformation conforme). Ce qui fait que si {V(x,y) = constante} représente les courbes de même potentiel, alors {φ(x,y) = constante} représente les lignes de champs électrique en électrostatique

Equation de Poisson

Si le membre de droite est une fonction donnée f(x,y,z), on obtient l'équation de Poisson :