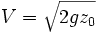Chute libre (physique) - Définition

Une chute libre est un mouvement accéléré sous le seul effet de la pesanteur. On distingue la simple chute dans un champ de pesanteur uniforme au voisinage de la Terre (Galilée, 1605), et la chute céleste (Lois de Kepler), dont Sir Isaac Newton fera la synthèse en 1687.

Il est convenu que les autres forces agissant sur le corps, sont négligées (pour plus de précisions, voir déviation vers l'Est), en particulier la résistance de l'air. Pour le cas où l'on considère la résistance de l'air, on parle de chute avec résistance de l'air.

Exemples de chutes libres proches

• la chute libre de Galilée (1602), depuis la tour de Pise.
• la pomme de Newton (1665) qui tombe de l'arbre, une fable très célèbre.
• l'expérience du tube de Newton.
• un ascenseur dont on aurait coupé le câble de suspension (tour d'impesanteur).
• une caravelle zero g.

Par opposition, des cas où d'autres forces que la pesanteur sont également présentes et doivent être prises en compte pour décrire le mouvement de l'objet, sont présentés ci-après :

• objet reposant sur une surface, par exemple horizontale : cas pour lequel la force exercée par cette surface compense le poids et agit de telle sorte que la force totale force résultante soit nulle, ne communiquant pas d'accélération à l'objet.
• avion ou feuille de papier planant : dans ces systèmes les forces de friction exercées par l'air sur l'objet jouent un rôle fondamental.

Chute ralentie

On peut aussi, comme l'a fait astucieusement Galilée, opérer une chute ralentie, pour mieux observer le mouvement : chute d'un palet sur du verglas incliné d'un angle α, chute sur des plans successifs, chute circulaire du pendule simple. Chute du pendule cycloïdal de Huygens. Chute ralentie de la machine d'Atwood ; il est évident que la loi de chute est différente, mais pas la loi de 1602 : la masse m n'intervient pas, car il y a compensation exacte entre masse inerte et masse grave !

Chute libre sans vitesse initiale

En supposant que le corps n'est soumis qu'à la pesanteur, si un corps ponctuel P est lâché d'un point de cote z₀ sans vitesse initiale, alors :

a_z = − g (composante selon l'axe des z de l'accélération, deuxième loi de Newton)

v_z = − gt + V₀ = − gt (composante selon l'axe des z de la vitesse)

(composante selon l'axe des z de la position)

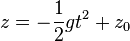
Avec :

• z la hauteur du corps par rapport au sol
• g l'accélération du champ de pesanteur terrestre (environ 9,81 m.s^-2)
• t le temps en secondes

La vitesse V à l'impact est donnée par:

Chute avec vitesse initiale

Il décrira une trajectoire parabolique (voir aussi parabole de sûreté).

Chute céleste

Si la vitesse initiale est appropriée, c'est-à-dire à la bonne valeur et la bonne orientation étant donnée la position initiale, la trajectoire peut être circulaire (cf. fenêtre de tir), comme elle l'est pour un satellite géostationnaire ; la Lune a plutôt un mouvement elliptique (en première approximation), très perturbé par l'influence du Soleil (la force de gravitation du Soleil sur la Lune est plus grande que la Force de gravitation de la Terre sur la Lune !).

Commentaire

Dans des systèmes en chute libre simple, les objets n'ont pas de poids apparent et flottent librement les uns par rapport aux autres. Pour cette raison, la notion de chute libre est employée dans les tours d'impesanteur, les avions en vol parabolique compensé (Caravelle 0-g) ou les systèmes en orbite pour simuler l'absence de gravité et étudier ses conséquences.

Contrairement à une idée reçue, les spationautes dans une station spatiale, ne flottent pas en apesanteur en raison d'une diminution de la gravitation due à leur éloignement de la Terre, mais parce que le système constitué par la station spatiale et eux-mêmes sont en chute libre (cf. Référentiel non inertiel, impesanteur).

La notion de chute libre est abordée en physique : on y explique la trajectoire parabolique ; puis la trajectoire balistique non parabolique, enfin la trajectoire d'un satellite (lois de Kepler). Bien sûr on fait remarquer que le raisonnement de Torricelli (1640 ?) pour la parabole tient toujours pour l'ellipse, le cas circulaire étant le plus simple à expliquer (Huygens, 1651) : c'est la célèbre figure du "funiculaire à rochets" : mouvement tangent + retombée "verticale" sur la trajectoire, etc. Newton utilisera beaucoup cette figure (1679-1687).

Vision relativiste

Dans la théorie de la relativité générale, la gravitation n'est pas une force mais une " déformation riemanienne de l'espace-temps " ; un objet dit en chute libre décrit simplement une géodésique de cet espace. On remarquera que la loi de Galilée (1602) [tous les corps ont même loi de chute] a été élevée au rang de Principe d'équivalence (de la masse inerte et de la masse grave) par Einstein en 1915, quand il a créé sa théorie.