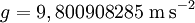Accélération - Définition

Dans la vie courante, on distingue trois événements que le physicien regroupe sous le seul concept d'accélération :

• aller plus vite (accélérer au sens commun plus restrictif : l'accélération est positive, c'est-à-dire que le vecteur accélération possède une composante dans le sens de la vitesse),
• aller moins vite (freiner ou décélérer ou ralentir dans le langage commun : l'accélération est négative, ou le vecteur accélération possède une composante opposée au sens de la vitesse)
• et changer de direction (tourner ou virer dans le langage commun : l'accélération est perpendiculaire à la vitesse, si celle-ci change de direction sans changer de norme)

Applications

Calcul de la distance parcourue

Par exemple, vous souhaitez calculer la distance parcourue par un solide en mouvement accéléré, dans le cas où l'accélération a est constante. Dans la formule ci-dessous, v₀ représente la vitesse initiale, Δt la durée du trajet et a l'accélération :

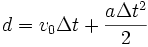
Exemple

Afin de déterminer la hauteur d'un pont, on lâche une pierre depuis le haut du-dit pont. Celle-ci met 2,5 secondes pour atteindre le sol. Quelle est la distance parcourue ?

On doit tenir compte que :

• la vitesse initiale est nulle ;
• l'accélération gravitationnelle est de 9,81 m·s⁻² ;
• l'on néglige le frottement de l'air qui réduit l'accélération proportionnellement à la vitesse instantanée.;

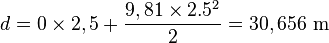
Accélération en mécanique dynamique

En dynamique, l'accélération subie par un corps est liée à la force totale exercée sur celui-ci par l'intermédiaire de la seconde loi de Newton (ou principe fondamental de la dynamique) selon laquelle

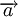
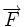
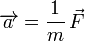
où m est la masse du corps.
Cette équation signifie que toute force appliquée à un objet produit automatiquement une accélération, quelle que soit la masse de cet objet.

Accélération moyenne

L'accélération moyenne a sur un intervalle de temps Δt est définie de la manière suivante :

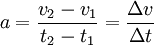
v₁ est la vitesse à l'instant t₁ et v₂ est la vitesse à l'instant t₂.

Accélération et gravité

La gravité provoque l'accélération d'une masse qui n'est soumise qu'à cette seule force, lors du mouvement qui par définition est appelé la chute libre. L'intensité de la gravité subie par un corps est donc exprimée sous la forme d'une accélération, notée . Afin de donner une valeur " parlante ", on exprime souvent une accélération par rapport à l'accélération moyenne de la gravité sur Terre, en g :

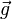
La relativité générale établit que la force de gravité ne se distingue pas localement (c'est-à-dire si l'on considère uniquement un point) d'une accélération, et que c'est la raison pour laquelle masse de gravitation et masse d'inertie ne peuvent être distinguées fonctionnellement. Il est important sur le plan conceptuel de connaître cette équivalence, beaucoup de physiciens utilisant pour cette raison, en abrégé, le terme accélération pour désigner indifféremment une modification de vitesse ou la présence dans un champ de gravité, même en l'absence apparente (dans l'espace 3D) de mouvement.

Variations d'accélération

Tout comme le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps on peut définir la dérivée de l'accélération par rapport au temps. Il s'agit du vecteur jerk qui permet ainsi de quantifier les variations d'accélération et qui est utilisé dans un certain nombre de domaines.

Accélération de la convergence en Mathématiques

Le terme est aussi utilisé en mathématiques, par exemple l'accélération de la convergence d'une suite (par des procédés comme le Delta-2 d'Aitken) signifie que l'écart entre la valeur des éléments de la suite et sa limite est plus petit que pour la suite initiale à un rang n donné.