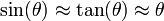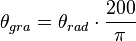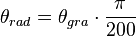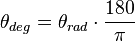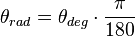Radian - Définition et Explications
Le radian (symbole : rad) est l'unité dérivée d'angle plan du système international (SI).
Considérons un secteur angulaire, formé de deux droites concourantes, et un cercle de rayon r centré à l'intersection des droites. Alors, la valeur de l'angle (En géométrie, la notion générale d'angle se décline en plusieurs concepts...) en radians est le rapport entre la longueur (La longueur d’un objet est la distance entre ses deux extrémités les plus...) L de l'arc de cercle (Un cercle est une courbe plane fermée constituée des points situés à égale...) intercepté par les droites et le rayon r.
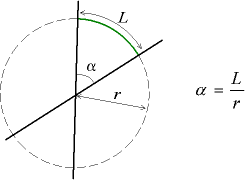
Un angle de 1 rad (L'abréviation rad désigne habituellement le radian, une unité d'angle.) est un angle, qui, ayant son sommet au centre d'un cercle, intercepte, sur la circonférence de ce cercle, un arc d'une longueur égale à celle du rayon du cercle. Un cercle complet représente un angle de 2π rad, appelé angle plein.
L'utilisation des radians est impérative lorsque l'on dérive ou intègre une fonction trigonométrique : en effet, l'angle pouvant se retrouver en facteur, seule la valeur en radians a un sens (SENS (Strategies for Engineered Negligible Senescence) est un projet scientifique qui a pour but...).
Autre caractéristique précieuse du radian (Le radian (symbole : rad) est l'unité dérivée d'angle plan du système international (SI).): pour des angles θ d'une valeur inférieure à 0,1 radian ou 5,5 grades ou 5 degrés, l'approximation (Une approximation est une représentation grossière c'est-à-dire manquant de...) suivante est valable à 1% près:
Il n'y a aucune formule de ce genre avec les valeurs en grades et degrés.
Les formules de conversion entre les grades et les radians sont :
Les formules de conversion entre les degrés et les radians sont :
Voici quelques angles particuliers et leur équivalence avec les grades et degrés :
| nom de l'angle | valeur en rad | valeur en g | valeur en ° |
|---|---|---|---|
| angle nul | 0 rad | 0g | 0° |
| milliradian | 1 mrad | 0g 6c 36cc 61ccc | 0°3′26″15? |
| π/4 rad | 50g | 45° | |
| radian | 1 rad | 63g 66c 19cc 77ccc | 57°17′44″48? |
| angle droit | π/2 rad | 100g | 90° |
| 3π/4 rad | 150g | 135° | |
| angle plat | π rad | 200g | 180° |
| 5π/4 rad | 250g | 225° | |
| 3π/2 rad | 300g | 270° | |
| 7π/4 rad | 350g | 315° | |
| angle plein | 2π rad | 400g | 360° |