Théorème de Cantor - Définition

Le théorème de Cantor est un théorème mathématique, dans le domaine de la théorie des ensembles, qui doit son nom au mathématicien Georg Cantor.

Cantor démontre que, pour tout ensemble E, le cardinal de E est toujours strictement inférieur au cardinal de ensemble des parties de E.

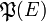
Lorsque E est un ensemble fini, le résultat est évident car le cardinal de E est le nombre d'éléments dans E et, si E contient n éléments, on démontre que l'ensemble des parties de E contient 2ⁿ éléments. Il est alors aisé de vérifier que, pour tout entier n, n < 2ⁿ.

Lorsque E est un ensemble infini, il faut repartir sur la comparaison des cardinaux.

si et seulement si, il existe une injection de A vers B.

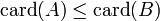
Cantor démontre que par un raisonnement par l'absurde : il suppose que , donc qu'il existe une injection de vers E et arrive à une contradiction.

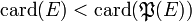
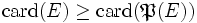
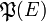
On appelle f cette injection. On construit alors un sous-ensemble B de E de la manière suivante:

soit x un élément de E,

• si x n'a pas d'antécédent par f alors x n'est pas dans B
• si x possède un antécédent par f, il est unique car f est injective. On note cet antécédent A_x. Si x appartient à A_x alors x n'est pas dans B, si x n'appartient pas à A_x alors x est dans B.

B est une partie de E, et possède donc une image par f, que l'on nomme y. La question qui se pose est : " y est-il ou non un élement de B? ". y a pour antécédent B.

si y est dans B alors, par construction de B , y n'appartient pas à son antécédent donc y n'appartient pas à ... B

si y n'est pas dans B, toujours d'après la construction de B, y doit appartenir à son antécédent, donc y appartient à ... B

Les deux hypothèses mènent à une contradiction donc il ne peut pas exister d'injection de vers E

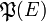
Ce type de raisonnement, que l'on appelle argument diagonal, a été utilisé par Russell (et Zermelo) pour le paradoxe de l'ensemble des ensembles qui ne s'appartiennent pas.