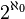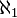Aleph-un - Définition

Aleph-un, parfois noté aleph1 ou (?, aleph, étant la première lettre de l'alphabet hébreu), est le cardinal de l'ensemble des ordinaux dénombrables.

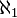
Dans la théorie ZF (théorie axiomatique des ensembles de Zermelo-Fraenkel sans l'axiome du choix), aucun cardinal n'est situé entre (aleph-zéro) et . Si l'axiome du choix est utilisé, il est possible de prouver que la classe des nombres cardinaux est totalement ordonnée et donc qu' est le deuxième plus petit nombre cardinal infini.

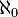
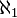
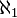
Dans ce dernier cas, si l'hypothèse du continu est validée, le cardinal d'un ensemble infini continu, comme l'ensemble des nombres réels , , est égal à .