Dudeneys Frage betraf die Umwandlung eines gleichseitigen Dreiecks in ein Quadrat durch Zerschneiden und Neuanordnung der Teile. Diese Art von Problem, bekannt als geometrische Zerlegung, interessiert sowohl Puzzle-Enthusiasten als auch Wissenschaftler. Die ursprüngliche Lösung erforderte vier Teile, aber bis jetzt hatte niemand bewiesen, dass es nicht besser geht.
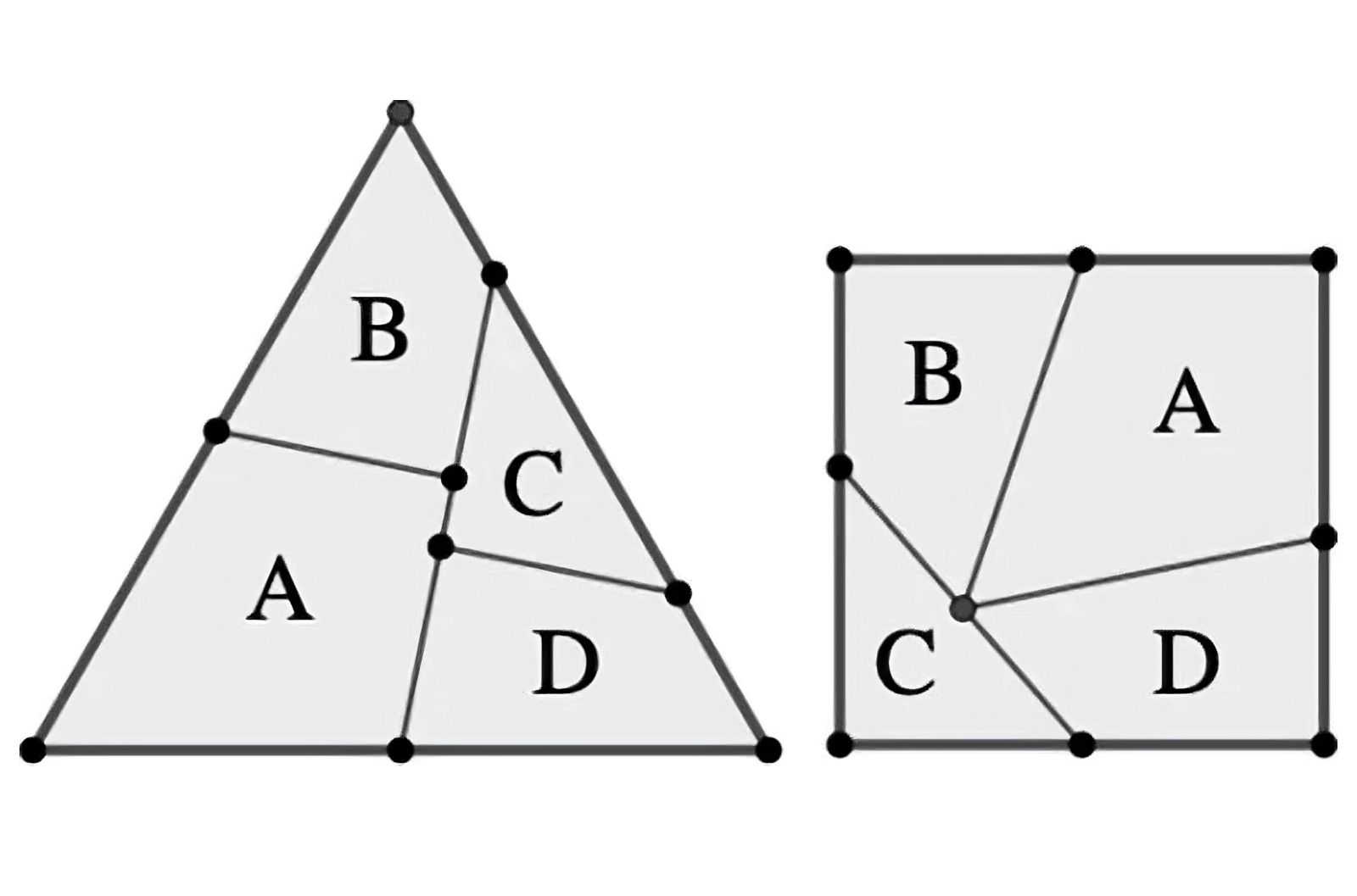
Illustration der Zerlegung eines gleichseitigen Dreiecks in ein Quadrat nach Dudeney's Methode.
Credit: Erik D. Demaine, Tonan Kamata, Ryuhei Uehara
Ein internationales Team hat kürzlich gezeigt, dass vier Teile tatsächlich das Minimum sind. Ihre Arbeit, veröffentlicht auf arXiv, basiert auf einer innovativen Methode mit Korrespondenzdiagrammen. Dieser Ansatz ermöglicht die Analyse der Beziehungen zwischen den Kanten und Ecken der geschnittenen Teile.
Die Forscher schlossen zunächst die Möglichkeit einer Lösung mit zwei Teilen aus und untersuchten dann systematisch alle möglichen Konfigurationen mit drei Teilen. Ihr Fazit ist eindeutig: Keine dieser Konfigurationen führt zu einem perfekten Quadrat. Dieser Beweis markiert einen bedeutenden Fortschritt im Verständnis von Zerlegungsproblemen.
Die Anwendungen dieser Forschung gehen über die reine Mathematik hinaus. Sie finden Widerhall in Bereichen wie Textildesign oder Materialherstellung. Die von den Wissenschaftlern entwickelte Methode könnte auch den Weg zur Lösung anderer ungelöster Zerlegungsprobleme ebnen.
Die Studie unterstreicht die Bedeutung von Korrespondenzdiagrammen bei der Analyse von Zerlegungen. Diese grafischen Werkzeuge ermöglichen die Visualisierung geometrischer Einschränkungen und den Beweis der Optimalität einer Lösung. Sie bieten somit eine neue Perspektive auf Probleme, die Mathematiker seit Jahrhunderten beschäftigen.
Diese Entdeckung beendet nicht nur ein Kapitel der Mathematikgeschichte. Sie schafft die Grundlage für zukünftige Forschungen, insbesondere in der Optimierung von Schneid- und Montageprozessen. Die Wissenschaftler planen bereits, ihre Methode auf andere geometrische Formen anzuwenden, was neue Fortschritte in diesem Bereich verspricht.
Was ist eine geometrische Zerlegung?
Eine geometrische Zerlegung besteht darin, eine Form in mehrere Teile zu schneiden, die neu angeordnet werden können, um eine andere Form zu bilden. Dieses Konzept, das bis in die Antike zurückreicht, ist sowohl ein mathematisches Spiel als auch ein Werkzeug zur Lösung praktischer Probleme.
Die einfachsten Zerlegungen betreffen Polygone wie Dreiecke und Quadrate. Das Ziel ist oft, die Anzahl der benötigten Teile zu minimieren, um von einer Form zur anderen zu gelangen. Dies erfordert ein tiefes Verständnis der geometrischen Eigenschaften der beteiligten Formen.
Über Rätsel hinaus haben geometrische Zerlegungen konkrete Anwendungen. Sie werden im Textildesign, in der industriellen Materialbearbeitung und sogar in der Kunst eingesetzt. Ihre Studie ermöglicht die Optimierung der Ressourcennutzung und die Reduzierung von Abfall.
Der Beweis der Optimalität einer Lösung, wie der von Dudeney, ist ein entscheidender Schritt. Er zeigt, dass die bestmögliche Lösung erreicht wurde, was für praktische Anwendungen wesentlich ist.
Wie funktionieren Korrespondenzdiagramme?
Korrespondenzdiagramme sind grafische Werkzeuge zur Analyse geometrischer Zerlegungen. Sie stellen die Beziehungen zwischen den Kanten und Ecken der geschnittenen Teile in Form von Graphen dar.
Im Fall der Zerlegung eines Dreiecks in ein Quadrat ermöglichen diese Diagramme die Visualisierung, wie die Teile zusammenpassen. Sie helfen, geometrische Einschränkungen zu identifizieren, die bestimmte Konfigurationen unmöglich machen.
Diese Methode ist besonders nützlich, um die Optimalität einer Lösung zu beweisen. Indem sie zeigen, dass keine Konfiguration mit weniger Teilen die Einschränkungen erfüllt, können Forscher behaupten, dass die Lösung die bestmögliche ist.
Korrespondenzdiagramme eröffnen neue Perspektiven zur Lösung komplexerer Zerlegungsprobleme. Ihre Anwendung könnte sich auf andere Bereiche wie Ingenieurstrukturentwurf oder industrielle Prozessoptimierung erstrecken.