Die erstaunliche Bewegungsgleichung von Katzen 🐱
Inspiriert von seinem eigenen Kater Eme, entwickelte er eine Gleichung, die die Bewegungen seines vierbeinigen Gefährten beschreibt und Katzen in den Mittelpunkt einer Demonstration der klassischen Mechanik stellt.
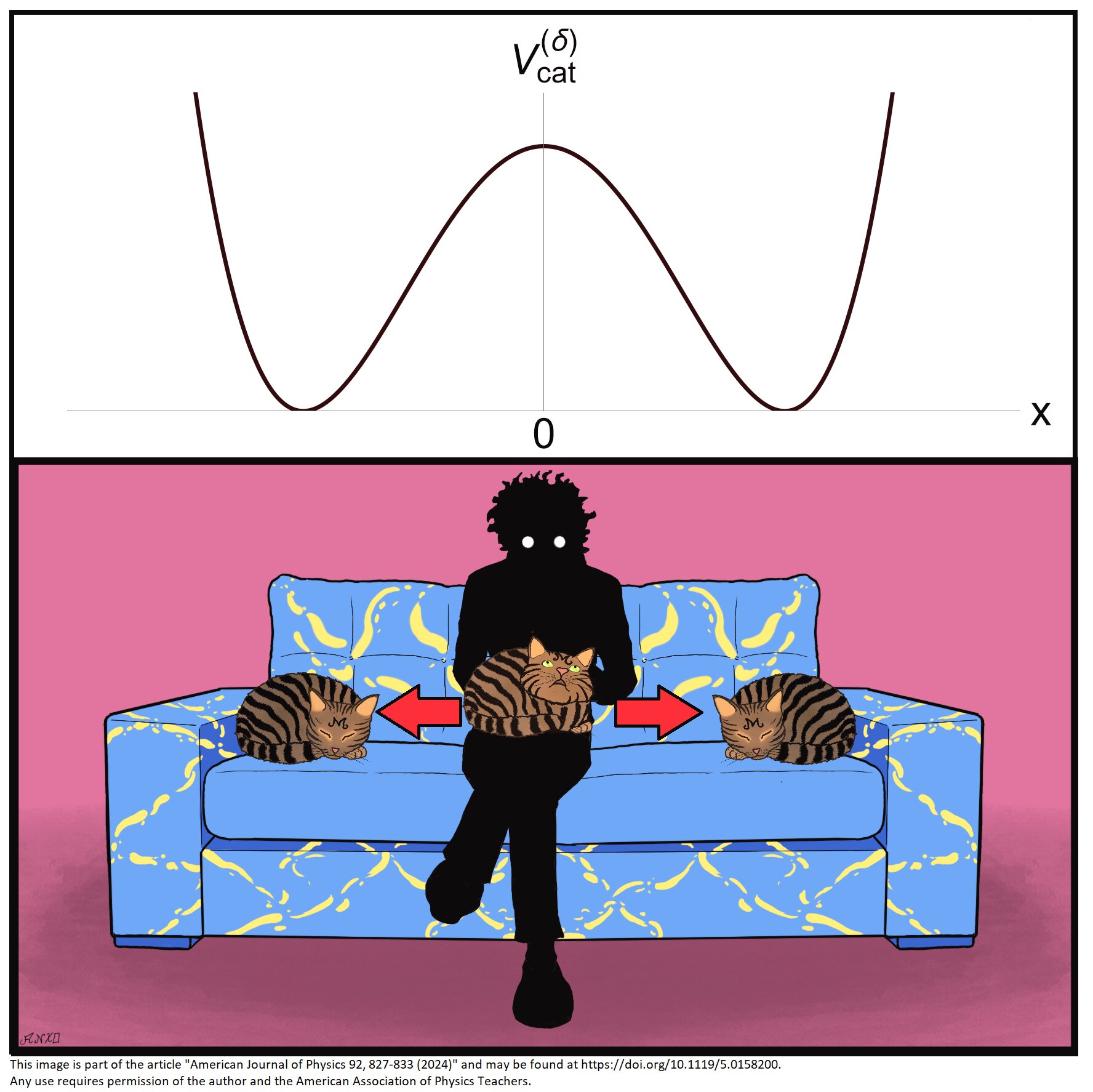
Detaillierte Darstellung der Bewegungsgleichung der Katze.
Quelle: American Journal of Physics
Mit dieser Studie will Biasi die Physik für die breite Öffentlichkeit verständlich machen. Ziel ist es, zu zeigen, wie grundlegende Gesetze auf alltägliche Situationen anwendbar sind, indem man ein Beispiel wählt, das jeder zu Hause beobachten kann: die Bewegungen einer Katze.
Um diese einzigartige Beziehung zwischen einer Katze und ihrem Menschen zu modellieren, verwendet Biasi eine einfache Gleichung. In dieser Modellierung wird die Katze als „Massenpunkt“ betrachtet, der sich in einem Potenzialtrichter bewegt, der durch die Anwesenheit des Menschen erzeugt wird. Durch Anwendung der Gesetze der Newtonschen Mechanik veranschaulicht die Studie mehrere typische Verhaltensweisen von Katzen, insbesondere ihre Neigung, in der Nähe ihres Besitzers zu bleiben.
Diese Studie entstand aus dem Wunsch, Physik unterhaltsam und zugänglich zu machen. Laut Biasi begann das Projekt als akademischer Scherz, inspiriert von den humorvollen Arbeiten einiger seiner Kollegen, nahm aber bald eine ernstere Wendung. Was anfangs wie ein Witz erschien, entwickelte sich zu einem wissenschaftlichen Modell, das nützlich ist, um die Physik durch einen spielerischen Ansatz zu verstehen.
Für die Entwicklung seiner Gleichung ließ sich Biasi von sieben Alltagsverhaltensweisen von Eme inspirieren. Unter diesen Verhaltensweisen stellt er fest, dass Katzen scheinbar „eine Kraft spüren“, die sie dazu bringt, sich in der Nähe ihres Menschen aufzuhalten. Dieses Modell ermöglicht es, die Interaktionen zwischen der Katze und ihrer Umgebung systematisch zu analysieren.
Die Gleichung, die Variablen wie die Masse der Katze und einen Reibungskoeffizienten zur Simulation ihrer Ermüdung einbezieht, bietet eine Interpretation ihrer Bewegungen in Abhängigkeit von ihrer Nähe zum Menschen. Durch diese Formel zeigt die Studie die notwendigen Schritte auf, um physikalische Modelle aus Alltagsbeobachtungen zu erstellen.
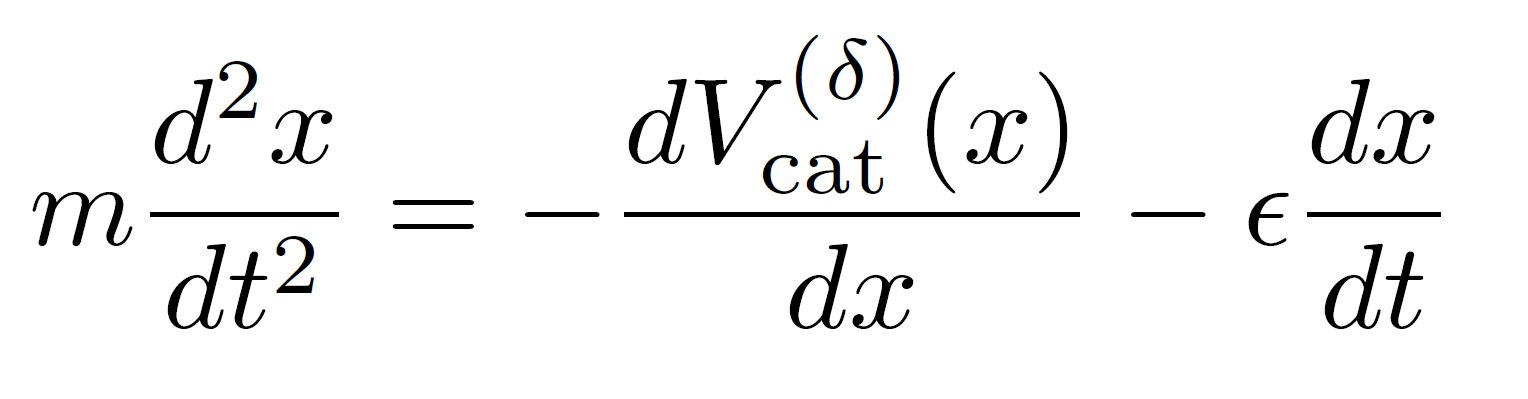
Die Bewegungsgleichung der Katze.
Quelle: Anxo Biasi
Die Analyse widmet sich auch Verhaltensweisen wie dem Schnurren, das Biasi als einen Stabilisationsmechanismus beschreibt. Er schlägt vor, dass das Schnurren einer Katze, die gestreichelt wird, den Menschen dazu ermutigt, weiter zu streicheln, wodurch ein positiver Verstärkungskreislauf zwischen den beiden entsteht.
Auch die berühmten „nächtlichen Verrücktheiten“ von Katzen, auch „Zoomies“ genannt, finden Platz im Modell. Während dieser Momente unkontrollierbarer Energieausbrüche erfordern die hektischen Bewegungen der Katze das Hinzufügen eines Zufallstermins zur Gleichung, der eine externe „Erzwingung“ darstellt, die die Spontaneität dieser Schübe einfängt.
Abgesehen vom unterhaltsamen Aspekt stellt diese Gleichung ein pädagogisches Werkzeug für den Unterricht in klassischer Mechanik dar. Biasi weist darauf hin, dass sein Modell genutzt werden könnte, um Anfängern die Grundlagen der Physik nahezubringen, indem gezeigt wird, wie komplexe Verhaltensweisen durch einfache Gesetze erklärt werden können.
Diese Gleichung stellt somit einen neuen Ansatz dar, um Physik für diejenigen zugänglicher zu machen, die vor der Abstraktion zurückscheuen. Durch die Verbindung von Wissenschaft und vertrautem Verhalten hofft Biasi, Neugier und Lernen durch ein so universelles Thema wie Katzen zu fördern.