Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)

Un echinacea montrant un développement en spirales de Fibonacci 21 et 34 (à gauche)
Spirales 8 et 13 sur une structure aplatie d'Ag/SiO2 (au centre et à droite)
Les nombres de Fibonacci proviennent d'une séquence numérique qui a fasciné le mathématicien italien Leonardo Fibonacci au début du 13ème siècle. Chaque entrée de la séquence est obtenue en ajoutant les deux nombres précédents: 0. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.... Ces nombres apparaissent fréquemment dans les configurations botaniques, comme l'agencement en spirale des pétales, des graines, des sépales ou des écailles sur des plantes telles que les pommes de pin, les ananas ou les tournesols. Par exemple, on peut trouver deux ensembles de lignes reliant les centres de chaque segment des pommes de pin, 13 dans le sens des aiguilles d'une montre et de 8 dans le sens inverse ; ou, dans le cas des spirales des tournesols, les combinaisons peuvent être 21 et 34, 34 et 55 et jusqu'à 89 et 144.
Les professeurs Cao Zexian, Li Chaorong et Zhang Xiaonan de l'Institut de physique du CAS, ont utilisé une microstructure d'environ 10 micromètres de diamètre, composée d'un noyau d'argent enveloppé d'oxyde de silicium. Ils ont chauffé un mélange d'Ag2O et de SiO sur un substrat maintenu à 1270°K, une température juste au-dessus du point de fusion de l'argent mais en dessous de celui du SiO2, et ont ensuite refroidi le système pas à pas. Les chercheurs ont découvert que l'enveloppe se rétrécissait beaucoup moins que le noyau, des structures chaotiques apparaissant alors sur cette enveloppe. Ces aspérités se présentaient sous différentes tailles et formes, selon la géométrie de la surface portante primaire, mais toujours de façon très uniforme.
Pour une microstructure sphérique, une configuration triangulaire répétitive est apparue, contenant quelques défauts lui permettant de couvrir la surface sphérique. Ces défauts prenaient la forme de cinq ou sept triangles entourant un sommet. Pour les microstructures coniques, le refroidissement conduisait à la formation d'aspérités arrangées en deux ensembles de spirales, tournant dans des directions opposées. Curieusement, les nombres de spirales dans chacun des ensembles étaient toujours des membres adjacents de la série de Fibonacci. Les chercheurs ont trouvé des positionnements de 5 et 8, 8 et 13, et 13 et 21 spirales.
C'est la première fois que des mosaïques triangulaires et des configurations en séries de Fibonacci sont développés avec des matériaux inorganiques à l'échelle du micron, selon les chercheurs du CAS. Ils ont également précisé le mécanisme et les conditions de formation de ces configurations sur la base d'une analyse de leurs caractéristiques structurales. "A partir de nos résultats nous voyons que c'est la géométrie de la surface portante, sur laquelle l'effort s'efforce d'obtenir une énergie de tension minimale, qui détermine la formation des différentes configurations", indique le professeur Cao. Les scientifiques présument que "les diverses configurations apparemment différentes intervenant en botanique peuvent être expliquées par le seul mécanisme de minimisation de l'énergie de tension totale sous une contrainte géométrique donnée, sans avoir besoin de recourir à des facteurs génétiques ou biochimiques".
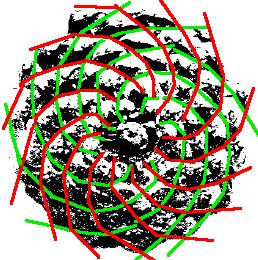
Spirales 8 et 13 sur une pomme de pin