Informatique quantique - Définition

Introduction

L'informatique quantique est le sous-domaine de l'informatique qui traite des ordinateurs quantiques utilisant des phénomènes de la mécanique quantique, par opposition à ceux de l'électricité exclusivement, pour l'informatique dite « classique ». Les phénomènes quantiques utiles sont l'intrication quantique et la superposition. Les opérations ne sont plus basées sur la manipulation de bits, mais de qubits.

Histoire

Fondation

Selon la loi de Moore, la puissance des ordinateurs augmente exponentiellement. Voyant cette « loi » possiblement devenir fausse à court terme, une solution est de changer de paradigme pour se tourner vers l'informatique quantique.

Par contre, selon la thèse de Church, tout calcul devrait être faisable efficacement sur une machine de Turing, alors qu'il ne semble pas possible de simuler un calculateur quantique avec une machine de Turing. Dans un premier temps, un autre type d'ordinateur semblait avoir contredit cette thèse, le calculateur analogique. Cette contradiction apparente a néanmoins été rapidement réfutée parce que la question du bruit n'avait pas été abordée, et la surpuissance supposée du calculateur analogique est maintenant nullifiée.

La prise en compte du bruit est donc un des premiers défis du calculateur quantique. En particulier, la théorie de l'information quantique traite des codes correcteurs quantiques et du calcul quantique avec tolérance d'erreurs.

Résultats non négatifs

Deux résultats des années 1990 indiquent que les ordinateurs quantiques pourraient être plus puissants que les machines de Turing, et même des machines de Turing probabilistes. En 1994, Peter Shor découvre l'algorithme de Shor qui permet de calculer efficacement la décomposition en produit de facteurs premiers et le logarithme discret. En 1995, Lov Grover découvre l'algorithme de Grover qui permet de faire efficacement une recherche dans un espace non structuré.

Les problèmes résolus par l'algorithme de Shor n'ont pas de solution efficace connue sur un ordinateur classique, bref, sur une machine de Turing. L'amélioration en efficacité provenant de l'algorithme de Grover n'est pas aussi significative, mais la très grande applicabilité des algorithmes de recherche implique l'importance du résultat.

Les bases mathématiques

Algèbre linéaire

Selon le principe de physique quantique, on conçoit le système physique comme un espace de Hilbert à d dimensions. Pour traiter ceci, les outils mathématiques principaux se trouvent en algèbre linéaire. La notation habituelle pour les vecteurs est remplacée par la notation bra-ket telle qu'expliquée ci-haut pour les états quantiques ψ, puisque ce sont ces états qui sont représentés par des vecteurs.

Le vecteur aussi appelé ket :

Le vecteur dual (autrement dit, transposé et conjugué) du ket, aussi appelé bra :

Les matrices typiquement utilisées sont : matrice hermitienne, matrice normale, matrice unitaire, matrice positive, matrice de densité, matrices de Pauli, matrice de Hadamard.

Matrices de densité

Les matrices de densité sont des objets mathématiques qui peuvent traiter tous les types d'états quantiques utiles à l'informatique quantique : l'état pur tout comme l'état mélangé, qui est un mélange d'états purs.

Opérations ou théorèmes utiles

Les matrices ont généralement la fonction d'opérateurs linéaires. De plus, certaines opérations sur ces opérateurs sont également définies.

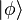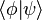• Opérations sur les vecteurs et  : produit scalaire , produit tensoriel 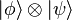ou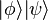
• Opérations sur les matrices A : conjugaison complexe A^* ou hermitienne A^t, transposition A^T, trace tr(A), diagonalisation
• Mesures : mesure quantique, distinction des états quantiques et mesure projective. Les mesures projectives sont des opérateurs qui sont des projecteurs (Observables).
• Théorème de décomposition spectrale, inégalité de Cauchy-Schwarz

Algèbre abstraite

Du domaine de l'algèbre abstraite, les Groupes de Lie suivants sont utiles: SU(2) et SO(3).

SU(2), le groupe spécial unitaire de degré 2

Le groupe SU(2) est isomorphe au groupe des quaternions de valeur absolue 1 et est donc identique à la sphère de dimension 3 S³. Comme les quaternions représentent les rotations dans l’espace à 3 dimensions, il existe un homorphisme surjectif de groupes de Lie SU(2) → SO(3,R) de noyau {+I,–I}. Les matrices dites matrices de Pauli forment une base de su(2). Ces matrices sont souvent utilisées en mécanique quantique pour représenter le spin des particules.

SO(3), le groupe orthogonal de degré 3 du corps

Le groupe SO(3), compris comme l’ensemble des rotations dans l’espace tridimensionnel, est appelé groupe des rotations.

En termes de topologie algébrique, pour n > 2, le groupe fondamental de SO(n) est le groupe cyclique d’ordre 2 et le groupe Spin Spin(n) est son recouvrement universel. Pour n=2, le groupe fondamental est le groupe cyclique infini et son recouvrement universel correspond à la droite des réels.